第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
计算下面各圆的面积。
① $ r= 7 $ 厘米
② $ d= 8 $ 分米
③ $ C= 12.56 $ 米
① $ r= 7 $ 厘米
② $ d= 8 $ 分米
③ $ C= 12.56 $ 米
答案:
解析:本题考查圆的面积的计算,需要用到圆的面积公式$S = \pi r^2$。对于已知半径$r$的,直接代入公式计算;对于已知直径$d$的,先求出半径$r=\frac{d}{2}$,再代入公式;对于已知周长$C$的,先根据$C = 2\pi r$求出半径$r=\frac{C}{2\pi}$,再代入面积公式。
①已知$r = 7$厘米,根据圆的面积公式$S=\pi r^2$,$\pi$取$3.14$,可得:
$S = 3.14×7^2$
$=3.14×49$
$ = 153.86$(平方厘米)
②已知$d = 8$分米,则半径$r=\frac{d}{2}=\frac{8}{2}=4$分米,再根据圆的面积公式可得:
$S = 3.14×4^2$
$=3.14×16$
$ = 50.24$(平方分米)
③已知$C = 12.56$米,由$C = 2\pi r$可得$r=\frac{C}{2\pi}$,$\pi$取$3.14$,则:
$r=\frac{12.56}{2×3.14}$
$=\frac{12.56}{6.28}$
$ = 2$(米)
再根据圆的面积公式可得:
$S = 3.14×2^2$
$=3.14×4$
$ = 12.56$(平方米)
答案:①$153.86$平方厘米;②$50.24$平方分米;③$12.56$平方米。
①已知$r = 7$厘米,根据圆的面积公式$S=\pi r^2$,$\pi$取$3.14$,可得:
$S = 3.14×7^2$
$=3.14×49$
$ = 153.86$(平方厘米)
②已知$d = 8$分米,则半径$r=\frac{d}{2}=\frac{8}{2}=4$分米,再根据圆的面积公式可得:
$S = 3.14×4^2$
$=3.14×16$
$ = 50.24$(平方分米)
③已知$C = 12.56$米,由$C = 2\pi r$可得$r=\frac{C}{2\pi}$,$\pi$取$3.14$,则:
$r=\frac{12.56}{2×3.14}$
$=\frac{12.56}{6.28}$
$ = 2$(米)
再根据圆的面积公式可得:
$S = 3.14×2^2$
$=3.14×4$
$ = 12.56$(平方米)
答案:①$153.86$平方厘米;②$50.24$平方分米;③$12.56$平方米。
① 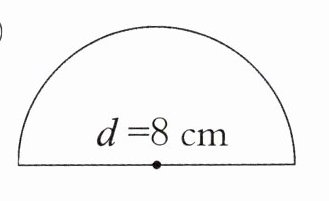
面积是(
周长是(
②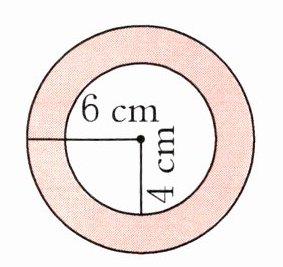
涂色部分的面积是(
③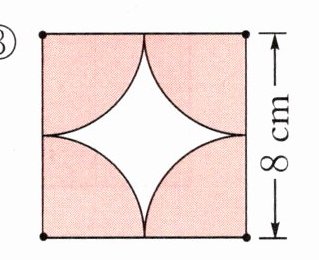
涂色部分的面积是(

面积是(
25.12
)$ \text{cm}^2 $,周长是(
20.56
)cm。②

涂色部分的面积是(
62.8
)$ \text{cm}^2 $。③

涂色部分的面积是(
13.76
)$ \text{cm}^2 $。
答案:
解析:本题主要考查圆的面积和周长公式以及通过图形变换求面积。对于①,已知半圆的直径,可根据圆的面积和周长公式求出半圆的面积和周长;对于②,涂色部分是圆环,可根据圆环面积公式求解;对于③,可通过正方形的面积减去四个四分之一圆的面积(即一个整圆的面积)得到涂色部分的面积。
答案:
①$25.12$;$20.56$
半圆的面积:$S=\frac{1}{2}\pi(\frac{d}{2})^2=\frac{1}{2}×3.14×(\frac{8}{2})^2=25.12cm^2$
半圆的周长:$C=\frac{1}{2}\pi d + d=\frac{1}{2}×3.14×8 + 8=20.56cm$
②$62.8$
圆环的面积:$S=\pi(R^2 - r^2)=3.14×(6^2 - 4^2)=62.8cm^2$
③$13.76$
正方形的面积:$S_{正方形}=8×8 = 64cm^2$
四个四分之一圆可拼成一个整圆,其面积:$S_{圆}=3.14×(\frac{8}{2})^2=50.24cm^2$
涂色部分的面积:$S = 64 - 50.24=13.76cm^2$
答案:
①$25.12$;$20.56$
半圆的面积:$S=\frac{1}{2}\pi(\frac{d}{2})^2=\frac{1}{2}×3.14×(\frac{8}{2})^2=25.12cm^2$
半圆的周长:$C=\frac{1}{2}\pi d + d=\frac{1}{2}×3.14×8 + 8=20.56cm$
②$62.8$
圆环的面积:$S=\pi(R^2 - r^2)=3.14×(6^2 - 4^2)=62.8cm^2$
③$13.76$
正方形的面积:$S_{正方形}=8×8 = 64cm^2$
四个四分之一圆可拼成一个整圆,其面积:$S_{圆}=3.14×(\frac{8}{2})^2=50.24cm^2$
涂色部分的面积:$S = 64 - 50.24=13.76cm^2$
① 公园草地上一个自动旋转喷灌装置的射程是 12 米,它能喷灌的面积是多少平方米?
答案:
解析:题目考查圆的面积计算。自动旋转喷灌装置的射程是圆的半径,根据圆的面积公式$S = \pi r^{2}$,其中$r$为半径,$\pi$取$3.14$,可求出喷灌面积。
答案:$3.14×12^{2}=3.14×144 = 452.16$(平方米)
答:它能喷灌的面积是$452.16$平方米。
答案:$3.14×12^{2}=3.14×144 = 452.16$(平方米)
答:它能喷灌的面积是$452.16$平方米。
② 一个大钟表的时针长 0.3 米,经过 24 小时,这根时针的尖端走了多少米?这根时针扫过的面积是多少平方米?
答案:
解析:
本题考查圆的周长和面积的计算。
时针在24小时内会完成两圈,即时针走过的路径是两个圆的周长,扫过的面积是两个圆的面积。
圆的周长公式为$C = 2\pi r$,其中$r$是半径,$\pi$取3.14。
圆的面积公式为$S = \pi r^{2}$。
时针的长度即为圆的半径,所以$r = 0.3$米。
计算时针尖端走过的距离:
时针走过的总路径为两个圆的周长,即:
$2 × (2\pi r) = 2 × 2 × 3.14 × 0.3 = 3.768$(米)。
计算时针扫过的面积:
时针扫过的总面积为两个圆的面积,即:
$2 × (\pi r^{2}) = 2 × 3.14 × (0.3)^{2} = 0.5652$(平方米)。
答案:
这根时针的尖端走了3.768米,这根时针扫过的面积是0.5652平方米。
本题考查圆的周长和面积的计算。
时针在24小时内会完成两圈,即时针走过的路径是两个圆的周长,扫过的面积是两个圆的面积。
圆的周长公式为$C = 2\pi r$,其中$r$是半径,$\pi$取3.14。
圆的面积公式为$S = \pi r^{2}$。
时针的长度即为圆的半径,所以$r = 0.3$米。
计算时针尖端走过的距离:
时针走过的总路径为两个圆的周长,即:
$2 × (2\pi r) = 2 × 2 × 3.14 × 0.3 = 3.768$(米)。
计算时针扫过的面积:
时针扫过的总面积为两个圆的面积,即:
$2 × (\pi r^{2}) = 2 × 3.14 × (0.3)^{2} = 0.5652$(平方米)。
答案:
这根时针的尖端走了3.768米,这根时针扫过的面积是0.5652平方米。
查看更多完整答案,请扫码查看


