第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1 看图填空。
①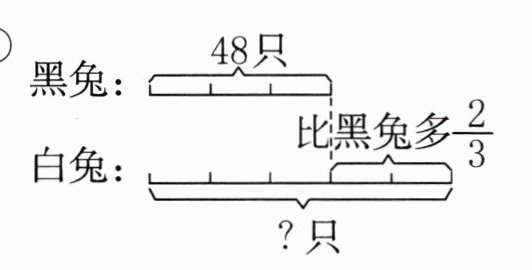
把(
②
把(
①

把(
黑兔
)的只数看作单位“1”,白兔比黑兔多(32
)只,白兔有(80
)只。②

把(
4月
)的产量看作单位“1”,5月的产量占4月的$\frac{(4
)}{(5
)}$,是(640
)台。
答案:
①黑兔;$32$;$80$。
解析:从图中可知把黑兔的只数看作单位“1”,白兔比黑兔多的只数为:$48×\frac{2}{3}=32$(只),白兔的只数为:$48 + 32=80$(只)。
②$4$月;$\frac{4}{5}$;$640$。
解析:把4月的产量看作单位“1”,5月的产量占4月的$1-\frac{1}{5}=\frac{4}{5}$,5月产量为$800×\frac{4}{5}=640$(台)。
解析:从图中可知把黑兔的只数看作单位“1”,白兔比黑兔多的只数为:$48×\frac{2}{3}=32$(只),白兔的只数为:$48 + 32=80$(只)。
②$4$月;$\frac{4}{5}$;$640$。
解析:把4月的产量看作单位“1”,5月的产量占4月的$1-\frac{1}{5}=\frac{4}{5}$,5月产量为$800×\frac{4}{5}=640$(台)。
① 3吨的$\frac{1}{3}$是(
② (
③ (
④ (
⑤ (
⑥ (
1
)吨。② (
4
)吨比3吨多$\frac{1}{3}$。③ (
2
)吨比3吨少$\frac{1}{3}$。④ (
35
)分钟比40分钟少$\frac{1}{8}$。⑤ (
70
)克比60克多$\frac{1}{6}$。⑥ (
$60\frac{1}{6}$
)克比60克多$\frac{1}{6}$克。
答案:
①
解析:根据分数乘法的意义,求一个数的几分之几是多少用乘法计算。
答案:$3×\frac{1}{3}=1$(吨)
②
解析:把$3$吨看作单位“$1$”,所求的吨数是$3$吨的$(1 + \frac{1}{3})$,根据分数乘法的意义求解。
答案:$3×(1 + \frac{1}{3})=3×\frac{4}{3}=4$(吨)
③
解析:把$3$吨看作单位“$1$”,所求的吨数是$3$吨的$(1 - \frac{1}{3})$,根据分数乘法的意义求解。
答案:$3×(1 - \frac{1}{3})=3×\frac{2}{3}=2$(吨)
④
解析:把$40$分钟看作单位“$1$”,所求的分钟数是$40$分钟的$(1 - \frac{1}{8})$,根据分数乘法的意义求解。
答案:$40×(1 - \frac{1}{8})=40×\frac{7}{8}=35$(分钟)
⑤
解析:把$60$克看作单位“$1$”,所求的克数是$60$克的$(1 + \frac{1}{6})$,根据分数乘法的意义求解。
答案:$60×(1 + \frac{1}{6})=60×\frac{7}{6}=70$(克)
⑥
解析:求比$60$克多$\frac{1}{6}$克是多少,用加法计算。
答案:$60+\frac{1}{6}=60\frac{1}{6}$(克)
解析:根据分数乘法的意义,求一个数的几分之几是多少用乘法计算。
答案:$3×\frac{1}{3}=1$(吨)
②
解析:把$3$吨看作单位“$1$”,所求的吨数是$3$吨的$(1 + \frac{1}{3})$,根据分数乘法的意义求解。
答案:$3×(1 + \frac{1}{3})=3×\frac{4}{3}=4$(吨)
③
解析:把$3$吨看作单位“$1$”,所求的吨数是$3$吨的$(1 - \frac{1}{3})$,根据分数乘法的意义求解。
答案:$3×(1 - \frac{1}{3})=3×\frac{2}{3}=2$(吨)
④
解析:把$40$分钟看作单位“$1$”,所求的分钟数是$40$分钟的$(1 - \frac{1}{8})$,根据分数乘法的意义求解。
答案:$40×(1 - \frac{1}{8})=40×\frac{7}{8}=35$(分钟)
⑤
解析:把$60$克看作单位“$1$”,所求的克数是$60$克的$(1 + \frac{1}{6})$,根据分数乘法的意义求解。
答案:$60×(1 + \frac{1}{6})=60×\frac{7}{6}=70$(克)
⑥
解析:求比$60$克多$\frac{1}{6}$克是多少,用加法计算。
答案:$60+\frac{1}{6}=60\frac{1}{6}$(克)
① 水果店购进橘子80千克,购进的香蕉的质量比橘子少$\frac{1}{8}$。这个水果店购进的香蕉比橘子少多少千克?购进香蕉多少千克?
答案:
香蕉比橘子少的质量:80×$\frac{1}{8}$=10(千克)
购进香蕉的质量:80-10=70(千克)
答:这个水果店购进的香蕉比橘子少10千克,购进香蕉70千克。
购进香蕉的质量:80-10=70(千克)
答:这个水果店购进的香蕉比橘子少10千克,购进香蕉70千克。
② 某服装厂计划生产西装4200套,实际比计划多生产$\frac{1}{7}$。该服装厂实际生产西装多少套?
答案:
解析:
本题考查的是分数的应用。
实际生产的数量由两部分组成:计划生产的数量和超出计划的数量。
首先,需要找出计划生产数量的$\frac{1}{7}$,即:
$4200×\frac{1}{7}=600$(套)
然后,将这个数量加到计划生产的数量上,得到实际生产的总数:
$4200+600=4800$(套)
所以,实际生产了4800套西装。
答案:4800套。
本题考查的是分数的应用。
实际生产的数量由两部分组成:计划生产的数量和超出计划的数量。
首先,需要找出计划生产数量的$\frac{1}{7}$,即:
$4200×\frac{1}{7}=600$(套)
然后,将这个数量加到计划生产的数量上,得到实际生产的总数:
$4200+600=4800$(套)
所以,实际生产了4800套西装。
答案:4800套。
查看更多完整答案,请扫码查看


