《2025年名师金典九年级数学全一册浙教版》

1. 对于二次函数$y= (x - 4)^{2}+2$,下列说法正确的是(C)
A.其图象开口向下
B.当$x＜4$时,$y随着x$的增大而增大
C.有最小值为$2$
D.其图象与$x$轴有两个交点

答案： C

2. 已知二次函数$y = -x^{2}+2x$,点$(-1,y_{1})$,$(0,y_{2})$,$(1.5,y_{3})$在该二次函数图象上,则(C)
A.$y_{2}＜y_{1}＜y_{3}$
B.$y_{1}＜y_{3}＜y_{2}$
C.$y_{1}＜y_{2}＜y_{3}$
D.$y_{3}＜y_{1}＜y_{2}$

答案： C

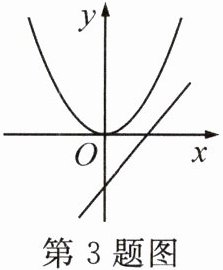
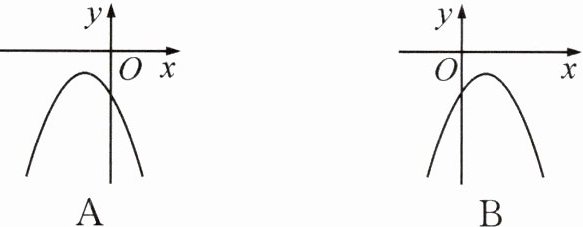
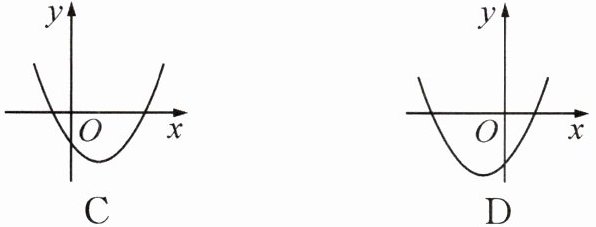
3. 在同一平面直角坐标系中,二次函数$y = ax^{2}与一次函数y = bx + c$的图象如图所示,则二次函数$y = ax^{2}+bx + c$的图象可能是(D).

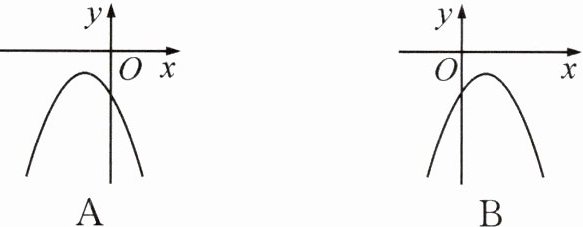
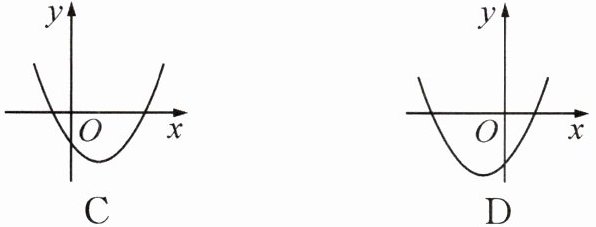
答案： D

4. 已知抛物线$y = ax^{2}+bx + c$如图所示,顶点坐标为$(4,6)$,则下列说法错误的是(C)
A.$b^{2}＞4ac$
B.$ax^{2}+bx + c\leqslant6$
C.若点$(2,m)(5,n)$在抛物线上,则$m＞n$
D.$8a + b = 0$

答案： C

5. 已知二次函数$y = -ax^{2}+2ax + 3$($a＞0$).若点$P(m,3)$在该函数的图象上,且$m\neq0$,则$m$的值为2.

答案： 2

6. 已知二次函数$y = x^{2}+bx + c的图象经过点(6,c)$,点$A(x_{1},y_{1})$,$B(5,y_{2})$在该函数图象上.当$m - 1\leqslant x_{1}\leqslant m$时,若$y_{1}\leqslant y_{2}$,则$m$的取值范围是____2≤m≤5.

答案： 2≤m≤5

7. 已知关于$x的二次函数y = -x^{2}+2mx + n$($m$,$n$为常数).
(1)若该二次函数图象经过$A(1,0)$,$B(2,0)$两点,求二次函数的表达式.
(2)若$m + n = 1$,试说明该函数图象与$x$轴必有两个不同的交点.

答案： 7.解:
(1)将A(1,0),B(2,0)代入y=-x²+2mx+n,得
{-1+2m+n=0,
{-4+4m+n=0,
解得{m=3/2,
{n=-2,
∴二次函数的表达式是y=-x²+3x-2.
(2)
∵m+n=1,
∴n=1-m,
∴函数表达式为y=-x²+2mx+1-m.
∵Δ=(2m)²-4×(-1)×(1-m)=(2m-1)²+3＞0,
∴该函数图象与x轴必有两个不同的交点.

8. 二次函数$y_{1}= -(x + 1)(x - a - 7)的图象与x$轴有两个交点,且两个交点之间的距离为$9$.
(1)求$a$的值.
(2)若二次函数的图象与$x$轴的交点在原点两侧,一次函数$y_{2}= -x + b的图象与二次函数的图象交y$轴于同一点.
①求$b$的值.
②当$y_{1}＜y_{2}$时,求自变量$x$的取值范围.

答案： 8.解:
(1)
∵函数图象与x轴的交点坐标为(-1,0),(a+7,0),
∴|a+7+1|=9,解得a=1或a=-17.
(2)①由二次函数的图象与x轴的交点在原点两侧,可知a=1,
∴y₁=-(x+1)(x-8)=-x²+7x+8,
∴该函数图象与y轴的交点坐标为(0,8),
∴b=8.
②联立得方程组{y=-x²+7x+8,
{y=-x+8,
解得{x=0,或{x=8,
{y=8 {y=0,
结合函数图象可知当y₁＜y₂时,x＜0或x＞8.