10. 如图,在$Rt\triangle ABC$中$,∠B = 90^{\circ},AB = 4,BC = 6,$点D在BC边上,将点A绕点D顺时针旋转$90^{\circ}$得到点E,连结DE,CE。当$\triangle DCE$是等腰三角形时,BD的长为
$\frac{5}{3}$或$4\sqrt{3}-4$
。
答案:
$\frac{5}{3}$或$4\sqrt{3}-4$
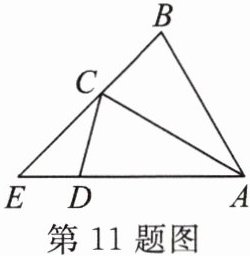
11. 如图,在$\triangle ABC$中,$AB = AC = 4$,将$\triangle ABC绕点A按逆时针方向旋转30^{\circ}得到\triangle ACD$,延长$AD交BC的延长线于点E$。
(1)求$∠E$的度数。
(2)求$DE$的长。
(1)求$∠E$的度数。
(2)求$DE$的长。

答案:
解:
(1)
∵将△ABC绕点A按逆时针方向旋转30°得到△ACD,
∴∠BAC=∠CAD=30°.
∵AB=AC,
∴∠B=75°,
∴∠E=180°−75°−60°=45°.
(2)如图,作CH⊥AE于点H.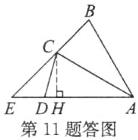
∵∠CAD=30°,AC=4,
∴CH=$\frac{AC}{2}$=2, 在Rt△ACH中,由勾股定理,得$AH=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$ 又由旋转可知AD=AC=4,
∴DH=4−2$\sqrt{3}$
∵∠E=45°,
∴EH=CH=2,
∴DE=EH−DH=2−(4−2$\sqrt{3}$)=2$\sqrt{3}$−2.
解:
(1)
∵将△ABC绕点A按逆时针方向旋转30°得到△ACD,
∴∠BAC=∠CAD=30°.
∵AB=AC,
∴∠B=75°,
∴∠E=180°−75°−60°=45°.
(2)如图,作CH⊥AE于点H.

∵∠CAD=30°,AC=4,
∴CH=$\frac{AC}{2}$=2, 在Rt△ACH中,由勾股定理,得$AH=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$ 又由旋转可知AD=AC=4,
∴DH=4−2$\sqrt{3}$
∵∠E=45°,
∴EH=CH=2,
∴DE=EH−DH=2−(4−2$\sqrt{3}$)=2$\sqrt{3}$−2.
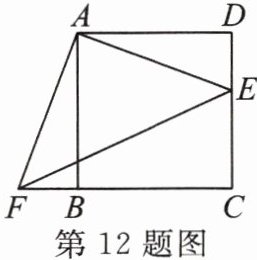
12. 如图,四边形$ABCD$是正方形,$\triangle ADE旋转后能与\triangle ABF$重合。
(1)判断$\triangle AEF$的形状,试说明理由。
(2)若$CF = 7$,$CE = 3$,求四边形$AECF$的面积。
(1)判断$\triangle AEF$的形状,试说明理由。
(2)若$CF = 7$,$CE = 3$,求四边形$AECF$的面积。

答案:
解:
(1)△AEF为等腰直角三角形.理由如下:
∵四边形ABCD为正方形,
∴AD=AB,∠BAD=∠D=∠ABC=90°.
∵△ADE旋转后能与△ABF重合,
∴AE=AF,∠EAF=∠DAB=90°,
∴△AEF为等腰直角三角形.
(2)
∵△ADE旋转后能与△ABF重合,
∴BF=DE,∠D=∠ABF=90°,S△ABF=S△ADE.
∴∠ABC+∠ABF=180°,
∴F点在CB的延长线上,
∴S四边形AECF=S△ABF+S四边形AECB=S△ADE+S四边形AECB=S正方形ABCD.
∵CF=7,
∴CB+BF=CB+DE=7, 而DE=CD−CE=CB−CE=CB−3,
∴CB+CB−3=7,解得CB=5,
∴S四边形AECF=S正方形ABCD=5²=25.
(1)△AEF为等腰直角三角形.理由如下:
∵四边形ABCD为正方形,
∴AD=AB,∠BAD=∠D=∠ABC=90°.
∵△ADE旋转后能与△ABF重合,
∴AE=AF,∠EAF=∠DAB=90°,
∴△AEF为等腰直角三角形.
(2)
∵△ADE旋转后能与△ABF重合,
∴BF=DE,∠D=∠ABF=90°,S△ABF=S△ADE.
∴∠ABC+∠ABF=180°,
∴F点在CB的延长线上,
∴S四边形AECF=S△ABF+S四边形AECB=S△ADE+S四边形AECB=S正方形ABCD.
∵CF=7,
∴CB+BF=CB+DE=7, 而DE=CD−CE=CB−CE=CB−3,
∴CB+CB−3=7,解得CB=5,
∴S四边形AECF=S正方形ABCD=5²=25.
13. 【猜测探究】
在$\triangle ABC$中,$∠ACB = \alpha$。$D是直线AB$上的一个动点,线段$CD绕点C逆时针旋转\alpha$,得到线段$CE$,连结$DE$,$BE$。
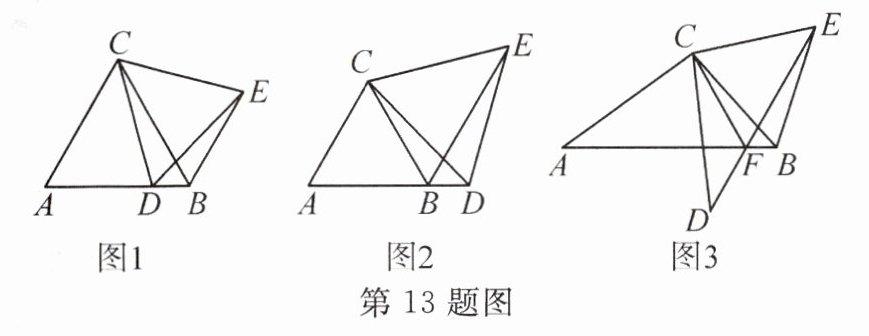
(1)如图1,当$CA = CB$,点$D在AB$边上运动时,线段$BD$,$AB和BE$之间的数量关系是____。
(2)如图2,当$CA = CB$,点$D运动到AB$的延长线上时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由。
【拓展应用】
(3)如图3,将$\triangle ABC绕点C逆时针旋转60^{\circ}得到\triangle DEC$,$DE交AB于点F$,连结$CF$。若$CF = 4$,$BF = 1$,$DF = 3$,求线段$DE$的长。
在$\triangle ABC$中,$∠ACB = \alpha$。$D是直线AB$上的一个动点,线段$CD绕点C逆时针旋转\alpha$,得到线段$CE$,连结$DE$,$BE$。
(1)如图1,当$CA = CB$,点$D在AB$边上运动时,线段$BD$,$AB和BE$之间的数量关系是____。
(2)如图2,当$CA = CB$,点$D运动到AB$的延长线上时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由。
【拓展应用】
(3)如图3,将$\triangle ABC绕点C逆时针旋转60^{\circ}得到\triangle DEC$,$DE交AB于点F$,连结$CF$。若$CF = 4$,$BF = 1$,$DF = 3$,求线段$DE$的长。

答案:
解:
(1)AB=BE+BD 解析:由旋转的性质,得CD=CE,∠ACB=∠DCE=α.
∵∠ACD+∠DCB=α,∠DCB +∠BCE=α,
∴∠ACD=∠BCE.又
∵CA=CB,
∴△ACD≌△BCE(SAS),
∴AD=BE;
∵AB=AD+BD,
∴AB=BE+BD.
(2)不成立,理由如下: 由旋转的性质,得∠ACB=∠DCE=α,CD=CE,
∴∠ACB+∠BCD=∠BCD+∠DCE,即∠ACD=∠BCE;又
∵CA=CB,
∴△ACD≌△BCE(SAS),
∴AD =BE;
∵AD=AB+BD,
∴BE=AB+BD.
(3)如图,在ED上取一点P,使EP =BF.由题意,得CB=CE,∠CBF =∠CEP,
∴△CFB≌△CPE(SAS),
∴CF=CP,∠FCB=∠PCE.由题意,得∠BCE=60°,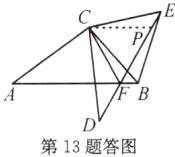
∴∠FCP=∠FCB+∠BCP=∠PCE+∠BCP=∠BCE =60°,
∴△FCP是等边三角形,
∴CF=FP,
∴DE=DF +FP+PE=DF+CF+BF=3+4+1=8,即线段DE的长为8.
解:
(1)AB=BE+BD 解析:由旋转的性质,得CD=CE,∠ACB=∠DCE=α.
∵∠ACD+∠DCB=α,∠DCB +∠BCE=α,
∴∠ACD=∠BCE.又
∵CA=CB,
∴△ACD≌△BCE(SAS),
∴AD=BE;
∵AB=AD+BD,
∴AB=BE+BD.
(2)不成立,理由如下: 由旋转的性质,得∠ACB=∠DCE=α,CD=CE,
∴∠ACB+∠BCD=∠BCD+∠DCE,即∠ACD=∠BCE;又
∵CA=CB,
∴△ACD≌△BCE(SAS),
∴AD =BE;
∵AD=AB+BD,
∴BE=AB+BD.
(3)如图,在ED上取一点P,使EP =BF.由题意,得CB=CE,∠CBF =∠CEP,
∴△CFB≌△CPE(SAS),
∴CF=CP,∠FCB=∠PCE.由题意,得∠BCE=60°,

∴∠FCP=∠FCB+∠BCP=∠PCE+∠BCP=∠BCE =60°,
∴△FCP是等边三角形,
∴CF=FP,
∴DE=DF +FP+PE=DF+CF+BF=3+4+1=8,即线段DE的长为8.
查看更多完整答案,请扫码查看


