《2025年名师金典九年级数学全一册浙教版》

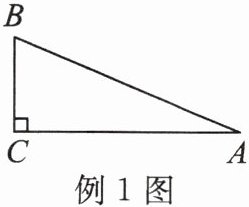
例1 如图,在Rt△ABC中,BC= 5,AB= 13,求sinA,cosA,tanA。

答案： 解:
∵在Rt△ABC中,BC=5,AB=13,
∴AC=12,
∴sinA=$\frac{BC}{AB}$=$\frac{5}{13}$,cosA=$\frac{AC}{AB}$=$\frac{12}{13}$,tanA=$\frac{BC}{AC}$=$\frac{5}{12}$.

变式1-1 在Rt△ABC中,∠C= 90°,∠A,∠B,∠C所对的边分别是a,b,c,则下列各式中,正确的是(C)
A.sinA= $\frac{a}{b}$
B.sinA= $\frac{b}{c}$
C.sinA= $\frac{a}{c}$
D.sinA= $\frac{b}{a}$

答案： C

例2 计算：
(1)tan²30°+2sin45°-sin60°·cos30°。
(2)2×$(-1)^{2021}$-$\frac{3}{sin60°}$+(sin45°-2)⁰+$\sqrt{12}$。

答案： 解:
(1)原式=($\frac{\sqrt{3}}{3}$)²+2×$\frac{\sqrt{2}}{2}$−$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{1}{3}$+$\sqrt{2}$−$\frac{3}{4}$=$\sqrt{2}$−$\frac{5}{12}$.
(2)原式=2×(−1)−3÷$\frac{\sqrt{3}}{2}$+1+2$\sqrt{3}$=−2−2$\sqrt{3}$+1+2$\sqrt{3}$=−1.

变式2-1 下列计算错误的有(C)
①sin60°-sin30°= sin30°；
②sin^245°+cos^245°= 1；
③3tan^260°= $\frac{1}{3}$；
④4tan30°= $\frac{cos30°}{sin30°}$。
A.1个
B.2个
C.3个
D.4个

答案： C

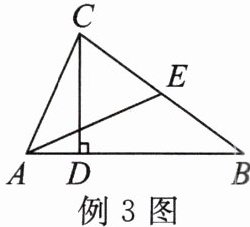
例3 如图,已知在△ABC中,CD⊥AB,垂足为D,AD= 2,BD= 6,tanB= $\frac{2}{3}$,E是边BC的中点。
(1)求边AC的长。
(2)求∠EAB的正弦值。

答案： 解:
(1)
∵CD⊥AB,
∴△ACD、△BCD均为直角三角形.在Rt△CDB中，
∵BD=6,tanB=$\frac{CD}{BD}$=$\frac{2}{3}$,
∴CD=4.在Rt△CDA中,AC=$\sqrt{CD²+AD²}$=$\sqrt{4²+2²}$=2$\sqrt{5}$.
(2)如图,过点E作EF⊥AB,垂足为F;
∵CD⊥AB,EF⊥AB,
∴CD//EF.又
∵E是边BC的中点，
∴EF是△BCD的中位线.
∴DF=BF=3,EF=$\frac{1}{2}$CD=2.
∴AF=AD+DF=5.在Rt△AEF中,AE=$\sqrt{AF²+EF²}$=$\sqrt{5²+2²}$=$\sqrt{29}$.
∴sin∠EAB=$\frac{EF}{AE}$=$\frac{2}{\sqrt{29}}$=$\frac{2\sqrt{29}}{29}$.

变式3-1 如图,矩形AOBC的顶点A,B在坐标轴上,点C的坐标是(-10,8),点D在AC上,将△BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于(D)
A.$\frac{3}{4}$
B.$\frac{3}{5}$
C.$\frac{\sqrt{3}}{3}$
D.$\frac{1}{2}$

答案： D