例1 在△ABC中,AB= 10,AC= 2√7,∠B= 30°,求△ABC的面积。
答案:
解:作AD⊥BC,交BC(或BC的延长线)于点D.①如图1,当AB,AC位于AD的异侧时,在Rt△ABD中,
∵∠B=30°,AB=10,
∴AD=ABsinB=5,BD=ABcosB=5√3.在Rt△ACD中,
∵AC=2√7,
∴CD=√(AC² - AD²)=√((2√7)² - 5²)=√3,则BC=BD + CD=6√3,
∴S△ABC = 1/2 × BC × AD = 1/2 × 6√3 × 5 = 15√3; ②如图2,当AB,AC在AD的同侧时,同①知AD=5,BD=5√3,CD=√3,则BC=BD - CD=4√3,
②如图2,当AB,AC在AD的同侧时,同①知AD=5,BD=5√3,CD=√3,则BC=BD - CD=4√3,
∴S△ABC = 1/2 × BC × AD = 1/2 × 4√3 × 5 = 10√3.综上所述,△ABC的面积是15√3或10√3.
解:作AD⊥BC,交BC(或BC的延长线)于点D.①如图1,当AB,AC位于AD的异侧时,在Rt△ABD中,
∵∠B=30°,AB=10,
∴AD=ABsinB=5,BD=ABcosB=5√3.在Rt△ACD中,
∵AC=2√7,
∴CD=√(AC² - AD²)=√((2√7)² - 5²)=√3,则BC=BD + CD=6√3,
∴S△ABC = 1/2 × BC × AD = 1/2 × 6√3 × 5 = 15√3;
 ②如图2,当AB,AC在AD的同侧时,同①知AD=5,BD=5√3,CD=√3,则BC=BD - CD=4√3,
②如图2,当AB,AC在AD的同侧时,同①知AD=5,BD=5√3,CD=√3,则BC=BD - CD=4√3,∴S△ABC = 1/2 × BC × AD = 1/2 × 4√3 × 5 = 10√3.综上所述,△ABC的面积是15√3或10√3.
变式1-1 已知,正方形ABCD的边长为2,点P是直线CD上一点。若DP= 1,则sin∠BPC的值是
$\frac{2\sqrt{5}}{5}$或$\frac{2\sqrt{13}}{13}$
。
答案:
情况一:点P在边CD上
∵正方形ABCD边长为2,DP=1,
∴PC=CD-DP=2-1=1,BC=2,∠BCD=90°。
在Rt△BPC中,BP=$\sqrt{BC^2+PC^2}=\sqrt{2^2+1^2}=\sqrt{5}$,
∴$\sin\angle BPC=\frac{BC}{BP}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$。
情况二:点P在CD延长线上
∵DP=1,
∴PC=CD+DP=2+1=3,BC=2,∠BCD=90°。
在Rt△BPC中,BP=$\sqrt{BC^2+PC^2}=\sqrt{2^2+3^2}=\sqrt{13}$,
∴$\sin\angle BPC=\frac{BC}{BP}=\frac{2}{\sqrt{13}}=\frac{2\sqrt{13}}{13}$。
$\frac{2\sqrt{5}}{5}$或$\frac{2\sqrt{13}}{13}$
∵正方形ABCD边长为2,DP=1,
∴PC=CD-DP=2-1=1,BC=2,∠BCD=90°。
在Rt△BPC中,BP=$\sqrt{BC^2+PC^2}=\sqrt{2^2+1^2}=\sqrt{5}$,
∴$\sin\angle BPC=\frac{BC}{BP}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$。
情况二:点P在CD延长线上
∵DP=1,
∴PC=CD+DP=2+1=3,BC=2,∠BCD=90°。
在Rt△BPC中,BP=$\sqrt{BC^2+PC^2}=\sqrt{2^2+3^2}=\sqrt{13}$,
∴$\sin\angle BPC=\frac{BC}{BP}=\frac{2}{\sqrt{13}}=\frac{2\sqrt{13}}{13}$。
$\frac{2\sqrt{5}}{5}$或$\frac{2\sqrt{13}}{13}$
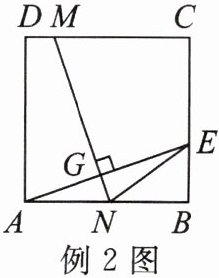
例2 如图,四边形ABCD为正方形,E为BC上一点,若将正方形折叠,使点A与点E重合,则折痕为MN。若∠AEN= α,且tanα= 1/3,DC+CE= 10。
(1)求△ANE的面积。
(2)求sin2α的值。
(1)求△ANE的面积。
(2)求sin2α的值。

答案:
解:
(1)由折叠的性质可知MN垂直平分AE,
∴AN=EN,
∴∠EAN=∠AEN=α,
∴tan∠EAB = tanα = 1/3.设BE=a,则AB=3a,又
∵四边形ABCD是正方形,
∴AB=CD=3a,CE=2a,
∵CD + CE=10,
∴3a + 2a=10,
∴a=2,
∴BE=2,AB=6,CE=4.设BN=x,则EN=AN=6 - x,在Rt△BNE中,BN² + BE² = NE²,即x² + 2² = (6 - x)²,解得x = 8/3,
∴AN = 10/3,
∴S△ANE = 1/2 × AN × BE = 10/3.
(2)
∵∠EAN=∠AEN=α,
∴∠ENB=2α,
∴sin2α = sin∠ENB = BE/EN = 3/5.
(1)由折叠的性质可知MN垂直平分AE,
∴AN=EN,
∴∠EAN=∠AEN=α,
∴tan∠EAB = tanα = 1/3.设BE=a,则AB=3a,又
∵四边形ABCD是正方形,
∴AB=CD=3a,CE=2a,
∵CD + CE=10,
∴3a + 2a=10,
∴a=2,
∴BE=2,AB=6,CE=4.设BN=x,则EN=AN=6 - x,在Rt△BNE中,BN² + BE² = NE²,即x² + 2² = (6 - x)²,解得x = 8/3,
∴AN = 10/3,
∴S△ANE = 1/2 × AN × BE = 10/3.
(2)
∵∠EAN=∠AEN=α,
∴∠ENB=2α,
∴sin2α = sin∠ENB = BE/EN = 3/5.
变式2-1 如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG//AD交AE于点G,若cosB= 1/4,则FG的长是(
A.3
B.8/3
C.2√15/3
D.5/2
B
)A.3
B.8/3
C.2√15/3
D.5/2
答案:
B
例3 在如图所示8×8的正方形网格中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD相交于点E,则∠AED的正切值是(
A.2
B.1/2
C.2/3
D.√5/5
B
)A.2
B.1/2
C.2/3
D.√5/5
答案:
B
变式3-1 如图,在每个小正方形边长都为1的5×3的正方形网格中,点A,B,C,D都在格点上,则sin∠1= ______。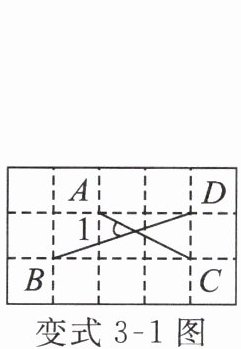

$\frac{\sqrt{2}}{2}$
答案:
连接格点构成等腰直角三角形,∠1为45°,$\sin45^\circ=\frac{\sqrt{2}}{2}$
$\frac{\sqrt{2}}{2}$
$\frac{\sqrt{2}}{2}$
1. 如图,在4×4正方形网格中,点A,B,C为网格格点,AD⊥BC,垂足为D,则sin∠BAD的值为(
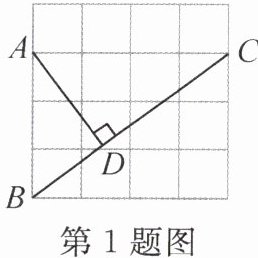
A.1/2
B.3/4
C.3/5
D.4/5
C
)
A.1/2
B.3/4
C.3/5
D.4/5
答案:
C
2. 在△ABC中,AB= 12√2,AC= 13,cosB= √2/2,则边BC的长为(
A.7
B.8
C.8或17
D.7或17
D
)A.7
B.8
C.8或17
D.7或17
答案:
D
查看更多完整答案,请扫码查看


