《2025年名师金典九年级数学全一册浙教版》

9. 如图,以点 O 为位似中心,将$△ABC缩小得到△A'B'C'$.若$AA'= 2OA'$,则$△ABC与△A'B'C'$的周长比为3:1.

答案： 3:1

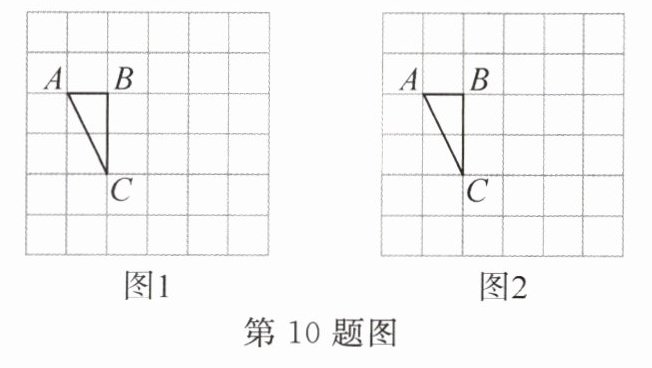
10. 如图,在$6×6$的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,$△ABC$的顶点均在格点上,按要求完成如下画图(要求仅用无刻度的直尺,且保留必要的画图痕迹).
(1)在图1中,以点 C 为位似中心.画出$△EFC$,使$△EFC与△ABC$位似,且位似比$EC:AC= k= 2$,点 E,F 为格点.
(2)在图2中,在 AC 边上找一个点 P,且满足$AP:CP= 3$

答案：
解:
(1)如图1,△EFC即为所求.
(2)如图2,取格点E,F,连结EF,交AC于点P,则点P 即为所求.

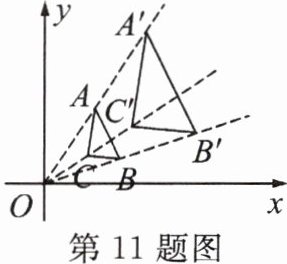
11. 如图,在平面直角坐标系中,$△ABC和△A'B'C'$是以坐标原点 O 为位似中心的位似图形,且$B(3,1),B'(6,2).$
(1)请你根据位似图形的特征,并结合点 B的坐标变换回答下列问题:
①若点 A 的坐标为$(2.5,3)$,则点$A'$的坐标为 (5,6).
②$△ABC与△A'B'C'$的相似比为 1:2.
(2)若$△ABC$的面积为 m,求$△A'B'C'$的面积(用含 m 的代数式表示).

解:∵△ABC与△A'B'C'的相似比为1:2,∴$\frac{S_{\triangle ABC}}{S_{\triangle A'B'C'}}=\frac{1}{4}$,而△ABC的面积为m,∴△A'B'C'的面积为4m.

答案： 解:
(1)①(5,6) 解析:
∵点B(3,1),B'(6,2),
∴△ABC与△A'B'C'的位似比为1:2.
∵点A(2.5,3),
∴点A'的坐标为(5,6). ②1:2
(2)
∵△ABC与△A'B'C'的相似比为1:2,
∴$\frac{S_{\triangle ABC}}{S_{\triangle A'B'C'}}=\frac{1}{4}$,而△ABC的面积为m,
∴△A'B'C'的面积为4m.

12. 如图,在平面直角坐标系中,正方形 ABCD与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比为$1:3$,点 A,B,E 在x轴上.
(1)若点 F 的坐标为$(4.5,3)$,直接写出点 C和点 A 的坐标.
(2)若正方形 BEFG 的边长为 6,求点 C 的坐标.

答案： 解:
(1)C(1.5,1),A(0.5,0) 解析:
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点F的坐标为(4.5,3),
∴点C的坐标为(1.5,1),
∴正方形ABCD的边长为1,
∴点A的坐标为(0.5,0).
(2)
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,
∴$\frac{AD}{BG}=\frac{1}{3}$.
∵BG=6,
∴AD=BC=AB=2.
∵AD//BG,
∴△OAD∽△OBG,
∴$\frac{AO}{BO}=\frac{AD}{BG}=\frac{1}{3}$,
∴$\frac{OA}{2+OA}=\frac{1}{3}$,
∴OA=1.
∴OB=3,
∴点C的坐标为(3,2).