9. 已知两个直角三角形的三边长分别为3,4,$m$和6,8,$n$,且这两个直角三角形不相似,则$m+n$的值为(
A.$10+\sqrt{7}或5+2\sqrt{7}$
B.15
C.$10+\sqrt{7}$
D.$15+3\sqrt{7}$
A
)A.$10+\sqrt{7}或5+2\sqrt{7}$
B.15
C.$10+\sqrt{7}$
D.$15+3\sqrt{7}$
答案:
A
10. 在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形. 如图,已知$\triangle ABC是6×4$的网格图形中的格点三角形,则该图中所有与$\triangle ABC$相似的格点三角形中,最大的三角形面积是
4.5
.
答案:
4.5
11. 我们定义:三边之比为$1:\sqrt{2}:\sqrt{5}$的三角形叫神奇三角形.
(1)如图1,$\triangle ABC$是正方形网格中的格点三角形,假设每个小正方形的边长为1,请说明$\triangle ABC$是神奇三角形,并直接写出$\angle ABC$的度数.
(2)请你在如图2所示的$5×2$的正方形网格中分别画出一个与(1)中$\triangle ABC$不全等的大小各不同的格点神奇三角形.

(1)如图1,$\triangle ABC$是正方形网格中的格点三角形,假设每个小正方形的边长为1,请说明$\triangle ABC$是神奇三角形,并直接写出$\angle ABC$的度数.
(2)请你在如图2所示的$5×2$的正方形网格中分别画出一个与(1)中$\triangle ABC$不全等的大小各不同的格点神奇三角形.

答案:
解:
(1)由题图,得$BC = \sqrt{1^{2}+1^{2}} = \sqrt{2}$,$AB = 2$,$AC = \sqrt{3^{2}+1^{2}} = \sqrt{10}$,$\therefore BC:AB:AC = \sqrt{2}:2:\sqrt{10} = 1:\sqrt{2}:\sqrt{5}$,$\therefore \triangle ABC$是神奇三角形,$\angle ABC = 135^{\circ}$。
(2)如图
解:
(1)由题图,得$BC = \sqrt{1^{2}+1^{2}} = \sqrt{2}$,$AB = 2$,$AC = \sqrt{3^{2}+1^{2}} = \sqrt{10}$,$\therefore BC:AB:AC = \sqrt{2}:2:\sqrt{10} = 1:\sqrt{2}:\sqrt{5}$,$\therefore \triangle ABC$是神奇三角形,$\angle ABC = 135^{\circ}$。
(2)如图

12. 如图,在四边形$ABCD$中,$AC$,$BD相交于点F$,点$E在BD$上,且$\frac{AB}{AE}= \frac{BC}{ED}= \frac{AC}{AD}$.
(1)试问:$\angle BAE与\angle CAD$相等吗?为什么?
(2)试判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.
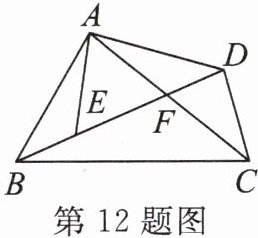
(1)试问:$\angle BAE与\angle CAD$相等吗?为什么?
(2)试判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.

答案:
解:
(1)$\angle BAE$与$\angle CAD$相等。理由:$\because \frac{AB}{AE}=\frac{BC}{ED}=\frac{AC}{AD}$,$\therefore \triangle ABC \backsim \triangle AED$,$\therefore \angle BAC = \angle EAD$,$\therefore \angle BAE = \angle CAD$。
(2)$\triangle ABE$与$\triangle ACD$相似。理由:$\because \frac{AB}{AE}=\frac{AC}{AD}$,$\therefore \frac{AB}{AC}=\frac{AE}{AD}$。又$\because \angle BAE = \angle CAD$,$\therefore \triangle ABE \backsim \triangle ACD$。
(1)$\angle BAE$与$\angle CAD$相等。理由:$\because \frac{AB}{AE}=\frac{BC}{ED}=\frac{AC}{AD}$,$\therefore \triangle ABC \backsim \triangle AED$,$\therefore \angle BAC = \angle EAD$,$\therefore \angle BAE = \angle CAD$。
(2)$\triangle ABE$与$\triangle ACD$相似。理由:$\because \frac{AB}{AE}=\frac{AC}{AD}$,$\therefore \frac{AB}{AC}=\frac{AE}{AD}$。又$\because \angle BAE = \angle CAD$,$\therefore \triangle ABE \backsim \triangle ACD$。
13. (分类讨论)一个钢筋三角架三边长分别是$20\mathrm{cm}$,$45\mathrm{cm}$,$55\mathrm{cm}$. 现要再做一个与其相似的钢筋三角架,而现在只有长为$30\mathrm{cm}和65\mathrm{cm}$的两根钢筋,要以其中一根为边,从另一根上截下两根(允许有余料)作为两边,有几种不同截法?分别加以说明.
答案:
解:有两种不同的截法。$\because$三角形的两边之和大于第三边,$\therefore$只能在65cm的钢筋上截。30cm的钢筋的对应边不同情况共有3种:①30cm钢筋对应最短边是20cm时,相似比为$\frac{30}{20}=\frac{3}{2}$,则$45×\frac{3}{2}=\frac{135}{2}$(cm),$55×\frac{3}{2}=\frac{165}{2}$(cm),$\frac{135}{2}+\frac{165}{2}=150$(cm)$>65$cm,不合题意,舍去;②30cm钢筋对应边是45cm时,相似比为$\frac{30}{45}=\frac{2}{3}$,则$20×\frac{2}{3}=\frac{40}{3}$(cm),$55×\frac{2}{3}=\frac{110}{3}$(cm),$\frac{40}{3}+\frac{110}{3}=\frac{150}{3}=50$(cm)$<65$cm,符合题意;③30cm钢筋对应边是55cm时,相似比为$\frac{30}{55}=\frac{6}{11}$,则$20×\frac{6}{11}=\frac{120}{11}$(cm),$45×\frac{6}{11}=\frac{270}{11}$(cm),$\frac{120}{11}+\frac{270}{11}=\frac{390}{11}$(cm)$<65$cm,符合题意。综上所述,有两种不同的截法,都在65cm钢筋上截,所截边长为$\frac{40}{3}$cm,$\frac{110}{3}$cm或$\frac{120}{11}$cm,$\frac{270}{11}$cm。
查看更多完整答案,请扫码查看


