《2025年名师金典九年级数学全一册浙教版》

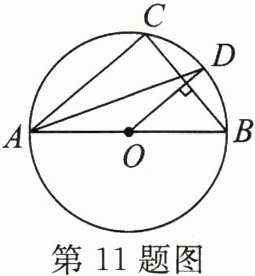
11. 如图,AB是$\odot O$的直径,C是圆上一点,连结CA,CB,过点O作弦BC的垂线,交$\overset{\frown }{BC}$于点D,连结AD.
(1)求证：$∠CAD= ∠BAD$.
(2)若$\odot O$的半径为1,$∠B= 50^{\circ }$,求$\overset{\frown }{AC}$的长.

答案：

(1)证明:
∵点$O$是圆心,$OD\perp BC$,
∴$\overset{\frown}{CD}=\overset{\frown}{BD}$,
∴$\angle CAD=\angle BAD$.
(2)解:如图，连结$CO$.
　　　　　　　　　　　　　　　　　　
∵$\angle B=50^\circ$,
∴$\angle AOC=100^\circ$,
∴$\overset{\frown}{AC}$的长为$\frac{100\pi×1}{180}=\frac{5\pi}{9}$.

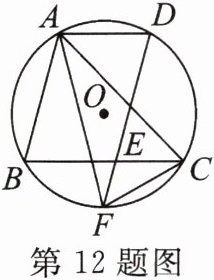
12. 如图,$\triangle ABC内接于\odot O$,$AD// BC交\odot O$于点D,$DF// AB$交BC于点E,交$\odot O$于点F,连结AF,CF.
(1)求证：$AC= AF$.
(2)若$\odot O$的半径为3,$∠CAF= 30^{\circ }$,求$\overset{\frown }{AC}$的长(结果保留π).

答案：

(1)证明:
∵$AD// BC$,$DF// AB$,
∴四边形$ABED$是平行四边形,
∴$\angle B=\angle D$.
∴$\overset{\frown}{AC}=\overset{\frown}{AF}$,
∴$AC=AF$.
(2)解:如图，连结$AO,CO$.
　　　　　　　　　　　　　　　　　　　
由
(1)得$AC=AF$,
∴$\angle AFC=\angle ACF$.又
∵$\angle CAF=30^\circ$,
∴$\angle AFC=\frac{180^\circ - 30^\circ}{2}=75^\circ$,
∴$\angle AOC=2\angle AFC=150^\circ$.
∴$\overset{\frown}{AC}$的长为$\frac{150\pi×3}{180}=\frac{5\pi}{2}$.

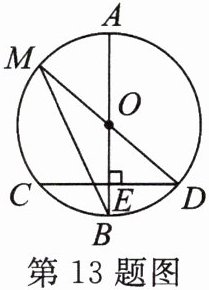
13. (方程思想)如图,AB是$\odot O$的直径,弦$CD⊥AB$于点E,点M在$\odot O$上,MD恰好经过圆心O,连结MB.
(1)根据条件,写出一对相等的线段或相等的角.
(2)若$CD= 16$,$BE= 4$,求$\odot O$的半径.
(3)若$\odot O$的半径是(2)中求得的半径,且$\overset{\frown }{CM}= \overset{\frown }{BD}$,求$\overset{\frown }{CAD}$的长.

答案：
解:
(1)答案不唯一,如$CE=DE$.
(2)设$\odot O$的半径为$r$.
∵$AB\perp CD$,
∴$CE=DE=\frac{1}{2}CD=\frac{1}{2}×16=8$.在$\text{Rt}\triangle ODE$中,$OE=OB - BE=r - 4$,$OD=r$,由勾股定理,得$OE^2+DE^2=OD^2$,即$(r - 4)^2+8^2=r^2$,解得$r=10$,
∴$\odot O$的半径为$10$.
(3)如图,连结$OC$.
　　　　　　　　　　　　　　　　　　　
∵$OM=OB$,
∴$\angle B=\angle M$,
∴$\angle DOB=\angle B+\angle M=2\angle B$.
∵$AB\perp CD$,
∴$\angle DOE+\angle D=90^\circ$,
∴$2\angle B+\angle D=90^\circ$.
∵$\overset{\frown}{CM}=\overset{\frown}{BD}$,
∴$\angle M=\angle D$,
∴$\angle B=\angle D$,
∴$2\angle D+\angle D=90^\circ$,
∴$\angle D=30^\circ$.
∵$OC=OD$,
∴$\angle C=\angle D=30^\circ$,
∴$\angle COD=120^\circ$,
∴$\overset{\frown}{CAD}$的长为$\frac{(360 - 120)\pi×10}{180}=\frac{40}{3}\pi$.