1. 如图,四边形ABCD是⊙O的内接四边形. 若∠A= 70°,则∠C的度数是(
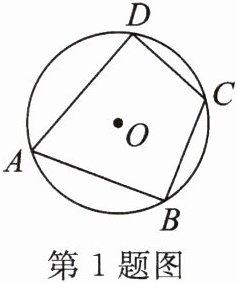
A.100°
B.110°
C.120°
D.130°
B
)
A.100°
B.110°
C.120°
D.130°
答案:
B
2. 在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是(
A.1:2:3:4
B.4:2:1:3
C.4:2:3:1
D.1:3:2:4
B
)A.1:2:3:4
B.4:2:1:3
C.4:2:3:1
D.1:3:2:4
答案:
B
3. 如图,四边形ABCD内接于⊙O,连结BD. 若$\overgroup{AC}= \overgroup{BC}$,∠BDC= 50°,则∠ADC的度数是(
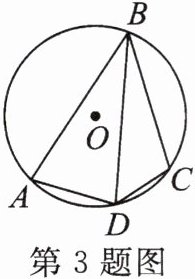
A.125°
B.130°
C.135°
D.140°
B
)
A.125°
B.130°
C.135°
D.140°
答案:
B
4. 如图,四边形ABCD为⊙O的内接四边形,已知∠C= ∠D,则AB与CD的位置关系是
AB//CD
.
答案:
AB//CD
5. 如图,四边形ABCD内接于⊙O,AD是⊙O的直径,连结BD. 若∠BCD= 100°,则∠ADB的度数为
10°
.
答案:
10°
6. 如图,四边形ABCD是⊙O的内接四边形,D是$\overgroup{AC}$的中点,E是$\overgroup{BC}$上的一点. 若∠CED= 35°,则∠ADC= ______°.
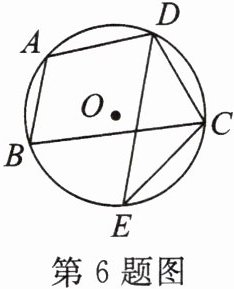

110
答案:
110
7. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点F在DB的延长线上,连结CF交⊙O于点G,连结DG,BG.
(1)若弧AC的度数是36°,求∠BGD的度数.
(2)求证:∠BGD= ∠BGF.
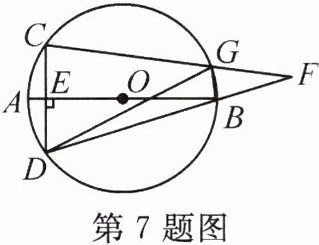
(1)若弧AC的度数是36°,求∠BGD的度数.
(2)求证:∠BGD= ∠BGF.

答案:
(1)解:
∵AB是⊙O的直径,CD⊥AB,
∴$\overset{\frown}{AC}=\overset{\frown}{AD}=36^{\circ}$.
∴$\overset{\frown}{BD}$的度数为180° - 36° = 144°,
∴∠BGD = $\frac{144^{\circ}}{2}$ = 72°.
(2)证明:
∵四边形CDBG是⊙O的内接四边形,
∴∠BGC + ∠CDB = 180°.
∵∠BGC + ∠BGF = 180°,
∴∠BGF = ∠CDB.
∵AB是⊙O的直径,CD⊥AB,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,
∴∠CDB = ∠BGD.
∴∠BGD = ∠BGF;
(1)解:
∵AB是⊙O的直径,CD⊥AB,
∴$\overset{\frown}{AC}=\overset{\frown}{AD}=36^{\circ}$.
∴$\overset{\frown}{BD}$的度数为180° - 36° = 144°,
∴∠BGD = $\frac{144^{\circ}}{2}$ = 72°.
(2)证明:
∵四边形CDBG是⊙O的内接四边形,
∴∠BGC + ∠CDB = 180°.
∵∠BGC + ∠BGF = 180°,
∴∠BGF = ∠CDB.
∵AB是⊙O的直径,CD⊥AB,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,
∴∠CDB = ∠BGD.
∴∠BGD = ∠BGF;
8. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E.
(1)若∠ADC= 86°,求∠CBE的度数.
(2)若AC= EC,求证:AD= BE.
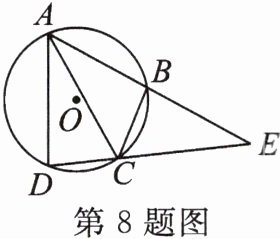
(1)若∠ADC= 86°,求∠CBE的度数.
(2)若AC= EC,求证:AD= BE.

答案:
(1)解:
∵四边形ABCD内接于⊙O,
∴∠ADC = ∠CBE;又
∵∠ADC = 86°,
∴∠CBE = 86°.
(2)证明:
∵AC = EC,
∴∠E = ∠CAE.
∵AC平分∠BAD,
∴∠DAC = ∠CAB.
∴∠DAC = ∠E;由
(1)可知,∠ADC = ∠CBE.在△ADC和△EBC中,$\begin{cases}∠ADC = ∠EBC \\ ∠DAC = ∠E \\ AC = EC\end{cases}$
∴△ADC ≌ △EBC(AAS),
∴AD = BE;
(1)解:
∵四边形ABCD内接于⊙O,
∴∠ADC = ∠CBE;又
∵∠ADC = 86°,
∴∠CBE = 86°.
(2)证明:
∵AC = EC,
∴∠E = ∠CAE.
∵AC平分∠BAD,
∴∠DAC = ∠CAB.
∴∠DAC = ∠E;由
(1)可知,∠ADC = ∠CBE.在△ADC和△EBC中,$\begin{cases}∠ADC = ∠EBC \\ ∠DAC = ∠E \\ AC = EC\end{cases}$
∴△ADC ≌ △EBC(AAS),
∴AD = BE;
查看更多完整答案,请扫码查看


