1. 若$\sin A= \frac {1}{2}$,则锐角$∠A= $(
A.$30^{\circ }$
B.$15^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
A
)A.$30^{\circ }$
B.$15^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
答案:
A
2. 在$\triangle ABC$中,$∠C= 90^{\circ }$,$\tan A= \sqrt {3}$,那么$\cos B$等于(
A.$\sqrt {3}$
B.$\frac {\sqrt {3}}{2}$
C.$\frac {1}{2}$
D.$\frac {\sqrt {2}}{2}$
B
)A.$\sqrt {3}$
B.$\frac {\sqrt {3}}{2}$
C.$\frac {1}{2}$
D.$\frac {\sqrt {2}}{2}$
答案:
B
3. 已知α为锐角,且$\tan (90^{\circ }-\alpha )= \sqrt {3}$,则α的度数为(
A.$60^{\circ }$
B.$30^{\circ }$
C.$45^{\circ }$
D.$75^{\circ }$
B
)A.$60^{\circ }$
B.$30^{\circ }$
C.$45^{\circ }$
D.$75^{\circ }$
答案:
B
4. $\cos \alpha =\frac {\sqrt {3}}{2}$,则$\alpha =$
30
$^{\circ }$。
答案:
30
5. 在$Rt\triangle ABC$中,$∠C= 90^{\circ }$,$∠A= 30^{\circ }$,$BC= 2$,则斜边上的中线长为
2
。
答案:
2
6. 在$\triangle ABC$中,若$| \cos A-\frac {1}{2}| +2(1-\tan B)^{2}= 0$,则$∠C$的度数是
75°
。
答案:
75°
7. 计算下列各式。
(1)$\tan 45^{\circ }+\cos 60^{\circ }-2\sin 30^{\circ }$。
(2)$\sqrt {3}\sin 60^{\circ }-3\tan 30^{\circ }+\cos ^{2}45^{\circ }$。
(1)$\tan 45^{\circ }+\cos 60^{\circ }-2\sin 30^{\circ }$。
(2)$\sqrt {3}\sin 60^{\circ }-3\tan 30^{\circ }+\cos ^{2}45^{\circ }$。
答案:
解:如图,过点 A 作 AD⊥BC 于点 D. 在 Rt△ACD 中,AC=6,∠C=30°,
∴AD=3,CD=3$\sqrt{3}$.
在 Rt△ABD 中,∠B=45°,AD =3,
∴BD=3,AB=3$\sqrt{2}$.
∴BC=3$\sqrt{3}$+3,AB=3$\sqrt{2}$.
∴AD=3,CD=3$\sqrt{3}$.
在 Rt△ABD 中,∠B=45°,AD =3,
∴BD=3,AB=3$\sqrt{2}$.
∴BC=3$\sqrt{3}$+3,AB=3$\sqrt{2}$.
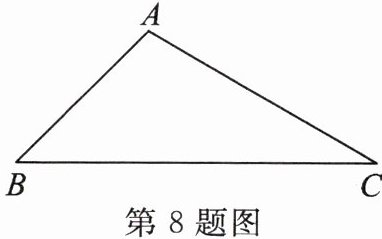
8. 如图,在$\triangle ABC$中,$∠B= 45^{\circ }$,$∠C= 30^{\circ }$,$AC= 6$,求$BC$,$AB$的长。

答案:
【解析】:本题可根据三角函数的定义,结合已知条件分别求出$AB$和$BC$的长。
在直角三角形中,正弦函数$\sin\alpha=\frac{对边}{斜边}$,余弦函数$\cos\alpha=\frac{邻边}{斜边}$,正切函数$\tan\alpha=\frac{对边}{邻边}$。
过点$A$作$AD\perp BC$于点$D$,将$\triangle ABC$分割成两个直角三角形$\triangle ABD$和$\triangle ACD$,在$Rt\triangle ACD$中,已知$\angle C = 30^{\circ}$,$AC = 6$,可先根据正弦函数求出$AD$的长,再根据余弦函数求出$CD$的长;在$Rt\triangle ABD$中,已知$\angle B = 45^{\circ}$,$AD$的长,可根据正切函数求出$BD$的长,进而求出$AB$和$BC$的长。
【答案】:解:过点$A$作$AD\perp BC$于点$D$。
在$Rt\triangle ACD$中,$\sin C=\frac{AD}{AC}$,$\cos C=\frac{CD}{AC}$。
因为$\angle C = 30^{\circ}$,$AC = 6$,所以$AD = AC\cdot\sin C = 6×\sin30^{\circ}=6×\frac{1}{2}= 3$;
$CD = AC\cdot\cos C = 6×\cos30^{\circ}=6×\frac{\sqrt{3}}{2}= 3\sqrt{3}$。
在$Rt\triangle ABD$中,$\angle B = 45^{\circ}$,$\tan B=\frac{AD}{BD}$,$\sin B=\frac{AD}{AB}$。
因为$\tan45^{\circ}= 1$,$AD = 3$,所以$BD = \frac{AD}{\tan B}=\frac{3}{\tan45^{\circ}} = 3$。
因为$\sin45^{\circ}=\frac{\sqrt{2}}{2}$,$AD = 3$,所以$AB = \frac{AD}{\sin B}=\frac{3}{\sin45^{\circ}} = 3\sqrt{2}$。
$BC = BD + CD = 3 + 3\sqrt{3}$。
综上,$AB$的长为$3\sqrt{2}$,$BC$的长为$3 + 3\sqrt{3}$。
在直角三角形中,正弦函数$\sin\alpha=\frac{对边}{斜边}$,余弦函数$\cos\alpha=\frac{邻边}{斜边}$,正切函数$\tan\alpha=\frac{对边}{邻边}$。
过点$A$作$AD\perp BC$于点$D$,将$\triangle ABC$分割成两个直角三角形$\triangle ABD$和$\triangle ACD$,在$Rt\triangle ACD$中,已知$\angle C = 30^{\circ}$,$AC = 6$,可先根据正弦函数求出$AD$的长,再根据余弦函数求出$CD$的长;在$Rt\triangle ABD$中,已知$\angle B = 45^{\circ}$,$AD$的长,可根据正切函数求出$BD$的长,进而求出$AB$和$BC$的长。
【答案】:解:过点$A$作$AD\perp BC$于点$D$。
在$Rt\triangle ACD$中,$\sin C=\frac{AD}{AC}$,$\cos C=\frac{CD}{AC}$。
因为$\angle C = 30^{\circ}$,$AC = 6$,所以$AD = AC\cdot\sin C = 6×\sin30^{\circ}=6×\frac{1}{2}= 3$;
$CD = AC\cdot\cos C = 6×\cos30^{\circ}=6×\frac{\sqrt{3}}{2}= 3\sqrt{3}$。
在$Rt\triangle ABD$中,$\angle B = 45^{\circ}$,$\tan B=\frac{AD}{BD}$,$\sin B=\frac{AD}{AB}$。
因为$\tan45^{\circ}= 1$,$AD = 3$,所以$BD = \frac{AD}{\tan B}=\frac{3}{\tan45^{\circ}} = 3$。
因为$\sin45^{\circ}=\frac{\sqrt{2}}{2}$,$AD = 3$,所以$AB = \frac{AD}{\sin B}=\frac{3}{\sin45^{\circ}} = 3\sqrt{2}$。
$BC = BD + CD = 3 + 3\sqrt{3}$。
综上,$AB$的长为$3\sqrt{2}$,$BC$的长为$3 + 3\sqrt{3}$。
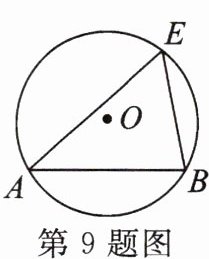
9. 如图,在$\odot O$中,弦$AB的长是12\sqrt {3}cm$,弦$AB的弦心距为6cm$,$E是\odot O$上一点。则$∠AEB$的度数为(
A.$60^{\circ }$
B.$45^{\circ }$
C.$30^{\circ }$
D.$80^{\circ }$
A
)
A.$60^{\circ }$
B.$45^{\circ }$
C.$30^{\circ }$
D.$80^{\circ }$
答案:
A
10. 如图,一渔船上的渔民在$A处看见灯塔M在北偏东60^{\circ }$方向,这艘渔船以$28km/h$的速度向正东航行,$0.5h到B$处,在$B处看见灯塔M在北偏东15^{\circ }$方向,此时,灯塔$M$与渔船的距离是(
A.$7\sqrt {2}km$
B.$14\sqrt {2}km$
C.$7km$
D.$14km$
A
)A.$7\sqrt {2}km$
B.$14\sqrt {2}km$
C.$7km$
D.$14km$
答案:
A
11. 已知$0^{\circ }<\alpha <90^{\circ }$,$0^{\circ }<\beta <90^{\circ }且\sin \alpha =\frac {1}{2}$,$\tan \beta =\sqrt {3}$,则$\cos (\beta -\alpha )= $
$\frac{\sqrt{3}}{2}$
。
答案:
$\frac{\sqrt{3}}{2}$
查看更多完整答案,请扫码查看


