《2025年名师金典九年级数学全一册浙教版》

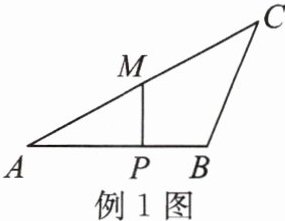
例1 如图,在$\triangle ABC$中,$\angle A= 30^{\circ}$,$AB= 6$,$AC= 8$。动点$P在线段AB上从顶点A$出发以每秒1个单位的速度向终点$B$运动,动点$M在线段AC上从顶点C$出发以每秒2个单位的速度向终点$A$运动,两点同时出发,有一点到达终点后两点都停止运动。设运动的时间为$x$秒,$\triangle APM的面积为y$。
(1)求$y关于x$的函数表达式。
(2)经过多少秒$\triangle APM$的面积最大？并求出最大值。

答案：
(1)过点P作PQ⊥AC于点Q，如图所示，
∴△APM在AM边上的高为PQ，由题意知AM = 8 - 2x，AP = x。
∵0 ≤ 8 - 2x ≤ 8，
∴0 ≤ x ≤ 4，
∵∠A = 30°，
∴PQ = $\frac{1}{2}$AP = $\frac{1}{2}$x，
∴y = $\frac{1}{2}$(8 - 2x)·$\frac{1}{2}$x = -$\frac{1}{2}$x² + 2x(0 ≤ x ≤ 4)。
(2)
∵y = -$\frac{1}{2}$x² + 2x = -$\frac{1}{2}$(x - 2)² + 2，
∴当x = 2时，y最大，为2，
∴经过2秒，△APM的面积最大，最大值为2。

变式1-1 如图,利用一个直角墙角修建一个$DC// AB的四边形储料场ABCD$,其中$\angle C= 120^{\circ}$。若新建墙$BC与CD$总长为12m,则该储料场$ABCD$的最大面积是(C)
A.$18m^{2}$
B.$18\sqrt{3}m^{2}$
C.$24\sqrt{3}m^{2}$
D.$\frac{25\sqrt{3}}{2}m^{2}$

答案： C

例2 如图,$P是抛物线y= x^{2}-x-4$在第四象限上的一点,过点$P分别向x轴和y$轴作垂线,垂足分别为$A$,$B$,则四边形$OAPB$周长的最大值为10。

答案： 10

变式2-1 在平面直角坐标系中,点$P的坐标为(0,2)$,点$M的坐标为(m-1,-\frac{3}{4}m-\frac{9}{4})$(其中$m$为实数)。当$MP$的长最小时,$m$的值为-$\frac{7}{5}$。

答案： -$\frac{7}{5}$

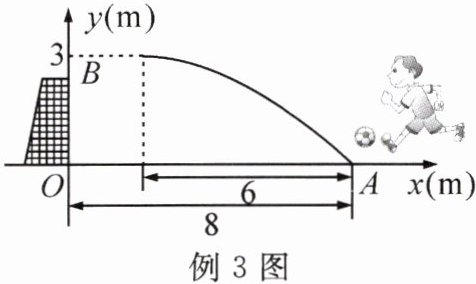
例3 在一次足球训练中,小明从球门正前方8m的$A$处射门,球射向球门的路线呈抛物线,当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m。已知球门高$OB$为2.44m。现以$O$为原点,建立如图所示的直角坐标系,并设抛物线的表达式为$y= a(x-h)^{2}+k$,其中$x(m)$是足球距球门的水平距离,$y(m)$是足球距地面的高度。
(1)求抛物线的表达式。
(2)通过计算判断球能否进球门。
(3)若抛物线的形状、最大高度均保持不变,且抛物线恰好经过点$O$正上方2.25m处,则该抛物线应向右平移几个单位？

答案：
(1)由题意得，抛物线的顶点坐标为(2,3)，经过点A(8,0)，
∴可设抛物线的表达式为y = a(x - 2)² + 3。把A(8,0)代入，得0 = 36a + 3，解得a = -$\frac{1}{12}$，
∴抛物线的表达式为y = -$\frac{1}{12}$(x - 2)² + 3。
(2)当x = 0时，y = -$\frac{1}{12}$×4 + 3 ≈ 2.67＞2.44，
∴球不能进球门。
(3)设平移后抛物线的表达式为y = -$\frac{1}{12}$(x + m)² + 3，把点(0,2.25)代入，得 -$\frac{1}{12}$m² + 3 = 2.25，整理，得m² = 9，解得m = 3(舍去)或m = -3，
∴平移后抛物线的顶点为点(3,3)。
∵原抛物线的顶点为点(2,3)，
∴抛物线应向右平移1个单位。