《2025年名师金典九年级数学全一册浙教版》

9. 如图,点A,B,C在⊙O上,P为$\overgroup{BC}$上任意一点,∠A= m,则∠D+∠E等于(C)
A.2m
B.$90^{\circ}-\frac{1}{2}\pi$
C.$180^{\circ}-2m$
D.$45^{\circ}+\frac{1}{2}\pi$

答案： C

10. 如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连结AE. 若∠ABC= 64°,则∠BAE的度数为52°.

答案： 52°

11. 如图,四边形ABCD内接于⊙O,AB= AC,BD⊥AC,垂足为E.
(1)若∠BAC= 40°,求∠ADC的度数.
(2)求证：∠BAC= 2∠DAC.

答案：
(1)解:
∵AB = AC,∠BAC = 40°,
∴∠ABC = ∠ACB = $\frac{180^{\circ}-40^{\circ}}{2}$ = 70°.
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC = 180° - ∠ABC = 110°.
(2)证明:
∵BD⊥AC,
∴∠AEB = ∠BEC = 90°,
∴∠ACB = 90° - ∠CBD.
∵AB = AC,
∴∠ABC = ∠ACB = 90° - ∠CBD,
∴∠BAC = 180° - 2∠ABC = 2∠CBD.
∵∠DAC = ∠CBD,
∴∠BAC = 2∠DAC.

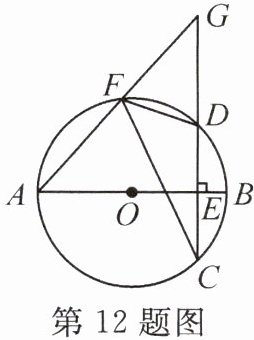
12. 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是$\overgroup{AD}$上的一点,AF,CD的延长线相交于点G,连结CF.
(1)若⊙O的半径为$3\sqrt{2}$,且∠DFC= 45°,求弦CD的长.
(2)求证：∠AFC= ∠DFG.

答案：

(1)解:如图1,连结OD,OC.
∵∠DFC = 45°,
∴∠DOC = 2∠DFC = 90°.在Rt△COD中,OC = OD = $3\sqrt{2}$,
∴CD = $\sqrt{OC^{2}+OD^{2}}$ = 6.
(2)证明:如图2,连结AC.
∵直径AB⊥CD,
∴$\overset{\frown}{AC}=\overset{\frown}{AD}$,
∴∠ACD = ∠AFC.
∵四边形ACDF内接于⊙O,
∴∠AFD + ∠ACD = 180°.
∵∠AFD + ∠DFG = 180°,
∴∠DFG = ∠ACD,
∴∠AFC = ∠DFG.

13.(转换化归)如图,⊙O为四边形ABCD的外接圆,其中$\overgroup{CD}= \overgroup{CB}$,CE⊥AB于点E.
(1)求证：AB= AD+2BE.
(2)若∠B= 60°,AD= 6,△ADC的面积为$\frac{15}{2}\sqrt{3}$,求AB的长.

答案：
(1)证明:如图,过点C作CF⊥AD交AD的延长线于点F.
∵$\overset{\frown}{CD}=\overset{\frown}{CB}$,
∴CD = CB,∠1 = ∠2.又
∵CF⊥AD,CE⊥AB,
∴∠AFC = ∠AEC = 90°,CF = CE;Rt△ACF ≌ Rt△ACE(AAS),Rt△CDF ≌ Rt△CBE(HL),
∴AF = AE,DF = BE,
∴AD + DF = AB - BE,
∴AB = AD + DF + BE = AD + 2BE,
∴AB = AD + 2BE.
(2)解:
∵$S_{\triangle ADC}=\frac{1}{2}AD× CF=\frac{15}{2}\sqrt{3}$,AD = 6,
∴CF = $\frac{5}{2}\sqrt{3}$.由
(1),得Rt△CDF ≌ Rt△CBE,
∴∠CDF = ∠B = 60°.在△CDF中,求得DF = $\frac{5}{2}$,
∴BE = DF = $\frac{5}{2}$,
∴AB = AD + 2BE = 6 + 2×$\frac{5}{2}$ = 11.