1. 如图,CD是⊙O的直径,点E在CD和弦AB上,且AE= BE,则下列结论不一定成立的是(
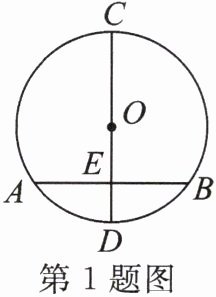
A.AB⊥CD
B.OE= DE
C.$\overset{\frown}{AC}= \overset{\frown}{BC}$
D.$\overset{\frown}{AD}= \overset{\frown}{BD}$
B
)
A.AB⊥CD
B.OE= DE
C.$\overset{\frown}{AC}= \overset{\frown}{BC}$
D.$\overset{\frown}{AD}= \overset{\frown}{BD}$
答案:
B
2. 如图,一条公路的拐弯处是一段圆弧AB,点O是这段弧所在的圆的圆心,AB= 20m,C是$\overset{\frown}{AB}$的中点,D是AB的中点,且CD= 5m,则这段弯路所在圆的半径为(
A.10m
B.12.5m
C.15m
D.17m
B
)A.10m
B.12.5m
C.15m
D.17m
答案:
B
3. 下列命题中,正确的个数有(
①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧。
A.1个
B.2个
C.3个
D.4个
B
)①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧。
A.1个
B.2个
C.3个
D.4个
答案:
B
4. 已知圆的半径为2,圆中一条弦长为$2\sqrt{3}$,则这条弦的中点到弦所对劣弧的中点的距离为
1
。
答案:
1
5. 如图,⊙O的弦AB,AC的夹角为50°,M,N分别为$\overset{\frown}{AB}和\overset{\frown}{AC}$的中点,OM,ON分别交AB,AC于点E,F,则∠MON的度数为
130°
。
答案:
130°
6. 如图,⊙O的直径CD= 10,AB是⊙O的弦,AB与CD的交点M是AB的中点,且DM:MC= 4:1,则AB的长是
8
。
答案:
8
7. 如图,在⊙O中,弦EF//CD,直径AB分别交CD,EF于点M,N,且A是$\overset{\frown}{EF}$的中点。求证:M是弦CD的中点。
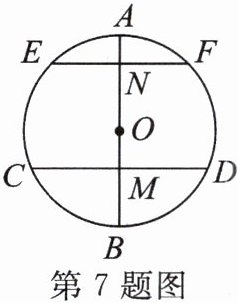

答案:
证明:
∵A是$\widehat{EF}$的中点,AB是$\odot O$的直径,
∴AB⊥EF;
∵EF//CD,
∴AB⊥CD,
∴CM=DM,即M是弦CD的中点.
∵A是$\widehat{EF}$的中点,AB是$\odot O$的直径,
∴AB⊥EF;
∵EF//CD,
∴AB⊥CD,
∴CM=DM,即M是弦CD的中点.
8. 如图,在残破的圆形工件上量得一条弦BC= 16,$\overset{\frown}{BC}$的中点D到BC的距离DE= 4,求这个圆形工件的半径。
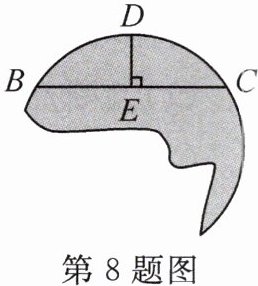

答案:
解:
∵DE⊥BC,DE平分弧BC,
∴圆心在直线DE上,设圆心为O,如图,连结OB,设圆的半径为R,则OE=R - 4.
∵OE⊥BC,
∴BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$×16=8.在Rt△OEB中,OB²=BE²+OE²,即R²=8²+(R−4)²,解得R=10,即这个圆形工件的半径是10.
∵DE⊥BC,DE平分弧BC,
∴圆心在直线DE上,设圆心为O,如图,连结OB,设圆的半径为R,则OE=R - 4.
∵OE⊥BC,
∴BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$×16=8.在Rt△OEB中,OB²=BE²+OE²,即R²=8²+(R−4)²,解得R=10,即这个圆形工件的半径是10.
查看更多完整答案,请扫码查看


