《2025年名师金典九年级数学全一册浙教版》

1. 将一个直角三角形的三边扩大到原来的3倍,得到的三角形一定是(A)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上三种情况都有可能

答案： A

2. 如图,正方形网格上的三角形(1)(2)(3)中与$\triangle ABC$相似的是(B)
A.(1)
B.(2)
C.(3)
D.都不与$\triangle ABC$相似

答案： B

3. 已知$\triangle ABC$的三边长分别为7.5,9和10.5,$\triangle DEF$的一边长为5. 若$\triangle DEF与\triangle ABC$相似,则$\triangle DEF$的另两边长可以是(C)
A.4,5
B.5,6
C.6,7
D.7,8

答案： C

4. 请你根据“三边对应成比例的两个三角形相似”补充一个条件：$\frac{AB}{MN}=\frac{AC}{MP}=\frac{BC}{NP}$,使得$\triangle ABC\backsim\triangle MNP$.

答案： $\frac{AB}{MN}=\frac{AC}{MP}=\frac{BC}{NP}$

5. 如图,在边长为1的正方形网格中有点$P$,$A$,$B$,$C$,则图中所形成的三角形中,相似的三角形是$\triangle APB \backsim \triangle CPA$.

答案： $\triangle APB \backsim \triangle CPA$

6. 两个三角形的三边长分别为4,5,6和6,7.5,9,则这两个三角形相似(填“相似”或“不相似”),理由是三边对应成比例的两个三角形相似.

答案： 相似　三边对应成比例的两个三角形相似

7. 如图,已知$\frac{BD}{BE}= \frac{AD}{CE}= \frac{AB}{BC}$. 求证：$\triangle ABC\backsim\triangle DBE$.

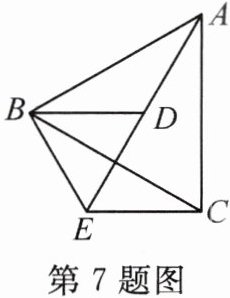
答案： 证明:$\because \frac{BD}{BE}=\frac{AD}{CE}=\frac{AB}{BC}$，$\therefore \triangle ABD \backsim \triangle CBE$，$\therefore \angle ABD = \angle CBE$，$\therefore \angle ABD + \angle DBC = \angle CBE + \angle DBC$，即$\angle ABC = \angle DBE$。又$\because \frac{AB}{BC}=\frac{BD}{BE}$，即$\frac{AB}{BD}=\frac{BC}{BE}$，$\therefore \triangle ABC \backsim \triangle DBE$。

8. 如图,在$8×8$的正方形网格中,$\triangle CAB和\triangle DEF$的顶点都在边长为1的小正方形的顶点上.
(1)填空：$AC= $$2\sqrt{5}$,$AB= $$2\sqrt{10}$.
(2)求$\angle ACB$的度数.解:$\because BC = \sqrt{2^{2}+4^{2}} = 2\sqrt{5}$，$AC = 2\sqrt{5}$，$AB = 2\sqrt{10}$，$\therefore AC^{2}+BC^{2}=AB^{2}$，$\therefore \angle ACB = 90^{\circ}$。
(3)判断$\triangle CAB和\triangle DEF$是否相似,并说明理由.解:$\triangle CAB$和$\triangle DEF$相似。理由如下:$DE = DF = \sqrt{1^{2}+2^{2}} = \sqrt{5}$，$EF = \sqrt{1^{2}+3^{2}} = \sqrt{10}$，$\therefore \frac{AC}{DE}=\frac{BC}{DF}=\frac{AB}{EF}=2$，$\therefore \triangle CAB \backsim \triangle DEF$。

答案：
(1)$2\sqrt{5}$　$2\sqrt{10}$
(2)解:$\because BC = \sqrt{2^{2}+4^{2}} = 2\sqrt{5}$，$AC = 2\sqrt{5}$，$AB = 2\sqrt{10}$，$\therefore AC^{2}+BC^{2}=AB^{2}$，$\therefore \angle ACB = 90^{\circ}$。
(3)解:$\triangle CAB$和$\triangle DEF$相似。理由如下:$DE = DF = \sqrt{1^{2}+2^{2}} = \sqrt{5}$，$EF = \sqrt{1^{2}+3^{2}} = \sqrt{10}$，$\therefore \frac{AC}{DE}=\frac{BC}{DF}=\frac{AB}{EF}=2$，$\therefore \triangle CAB \backsim \triangle DEF$。