《2025年名师金典九年级数学全一册浙教版》

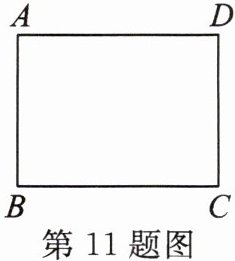
11. 圆圆在解答问题“如图,在矩形ABCD中,AB= 6,AD= 8,以A为圆心作⊙A,使得B,C,D三点中至少有一点在⊙A内,有一点在⊙A外,求⊙A的半径r的取值范围。”时,答案为“6＜r＜8”。圆圆的答案对吗？如果错误,请写出正确的解答过程。

答案：
解:圆圆的答案不正确.正确的解答过程如下:
　如图，连结AC.
∵四边形ABCD为矩形，
∴$BC=AD=8$，$\angle B=90^{\circ}$.
　　　　　　　　　　　　　　　　　
　根据勾股定理，得
　$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=10$，
∵B，C，D三点中至少有一点在$\odot A$内，有一点在$\odot A$外，
∴点B在$\odot A$内，点C在$\odot A$外，
∴$6＜r＜10$.

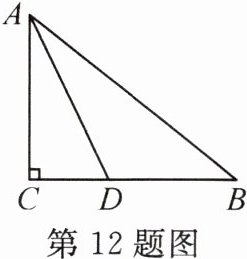
12. 如图,在Rt△ABC中,∠C= 90°,AD平分∠BAC。
(1)在AB边上找一点O,以点O为圆心,且过A,D两点作⊙O(不写作法,保留作图痕迹)。
(2)在(1)的条件下,若AB= 6,BD= $2\sqrt{3}$,求⊙O的半径。

答案：
解:
(1)如图，$\odot O$即为所求.
(2)如图，连结OD.设$\odot O$的半径为x，则$OA=OD=x$.
∵$AD$平分$\angle BAC$，
　　　　　　　　　　　　　　　
∴$\angle CAD=\angle BAD$.
∵$OA=OD$，
∴$\angle BAD=\angle ADO$，
∴$\angle ADO=\angle CAD$，
∴$OD// AC$，
∴$\angle ODB=\angle C=90^{\circ}$，
∴$OD^{2}+BD^{2}=OB^{2}$，即$x^{2}+(2\sqrt{3})^{2}=(6 - x)^{2}$，解得$x = 2$，
∴$\odot O$的半径为2.

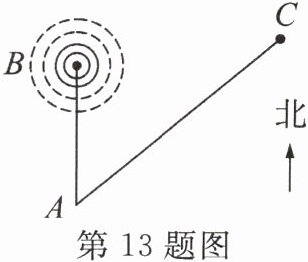
13. (数学建模)如图,城市A的正北方向50千米的B处,有一无线电信号发射塔。已知该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/时。
(1) 当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强。此时,班车到发射塔的距离是多少千米(离发射塔越近,信号越强)?
(2) 在(1)的条件下,班车从A城到C城共行驶2小时,请你判断到C城后还能接收到信号吗？请说明理由。

答案：
解:
(1)设班车行驶了0.5小时的时候到达M点，则$AM=60× 0.5 = 30$（千米）.根据此时接收信号最强，则$BM\perp AC$，如图.
　　　　　　　　　　　　　　　　　
　又$AB = 50$千米.
∴$BM=\sqrt{AB^{2}-AM^{2}} = 40$千米，即班车到发射塔的距离是40千米.
(2)能.理由如下:如图，连结BC.
∵$AC=60× 2 = 120$（千米），$AM = 30$千米，
∴$CM=AC - AM = 90$千米，
∴$BC=\sqrt{BM^{2}+CM^{2}} = 10\sqrt{97}$千米$＜100$千米，
∴到C城后还能接收到信号.