《2025年名师金典九年级数学全一册浙教版》

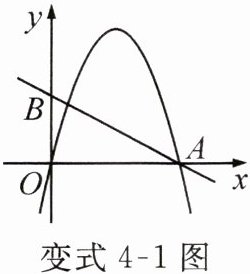
变式4-1 如图,直线$y = -\frac{1}{2}x + 2分别交x$轴,$y轴于点A,B$,抛物线$y = -x^{2}+mx经过点A$.
(1)求点$B$的坐标和抛物线的函数表达式.
(2)若抛物线向左平移$n个单位后经过点B$,求$n$的值.

答案：
(1)对于直线$y=-\frac{1}{2}x + 2$，令$x = 0$，则$y=2$，所以点$B$的坐标为$(0,2)$。
令$y = 0$，则$-\frac{1}{2}x + 2=0$，解得$x = 4$，所以点$A$的坐标为$(4,0)$。
因为抛物线$y=-x^{2}+mx$经过点$A(4,0)$，所以将$x = 4$，$y = 0$代入抛物线表达式得：$-4^{2}+4m=0$，即$-16 + 4m=0$，解得$m = 4$，所以抛物线的函数表达式为$y=-x^{2}+4x$。
(2)抛物线$y=-x^{2}+4x$向左平移$n$个单位后，其表达式变为$y=-(x + n)^{2}+4(x + n)$。
因为平移后的抛物线经过点$B(0,2)$，所以将$x = 0$，$y = 2$代入得：$-(0 + n)^{2}+4(0 + n)=2$，即$-n^{2}+4n=2$，整理得$n^{2}-4n + 2=0$。
解得$n=\frac{4\pm\sqrt{16 - 8}}{2}=\frac{4\pm2\sqrt{2}}{2}=2\pm\sqrt{2}$。
所以$n$的值为$2+\sqrt{2}$或$2-\sqrt{2}$。

1.抛物线$y = -\frac{1}{2}x^{2}+x + 1$经平移后,不可能得到的抛物线是(D)
A.$y = -\frac{1}{2}x^{2}+x$
B.$y = -\frac{1}{2}x^{2}-4$
C.$y = -\frac{1}{2}x^{2}+2025x - 2024$
D.$y = -x^{2}+x + 1$

答案： 【解析】：
本题主要考察二次函数抛物线平移的性质。
对于二次函数$y = ax^{2} + bx + c$，当抛物线进行平移时，其二次项系数$a$不会发生变化，只是$b$，$c$或常数项可能会发生变化。
因此，可以通过比较二次项系数来判断抛物线是否可以通过平移得到。
原抛物线方程为$y = -\frac{1}{2}x^{2} + x + 1$，其二次项系数为$-\frac{1}{2}$。
A选项：$y = -\frac{1}{2}x^{2} + x$，二次项系数也为$-\frac{1}{2}$，所以可能通过平移得到。
B选项：$y = -\frac{1}{2}x^{2} - 4$，二次项系数也为$-\frac{1}{2}$，所以可能通过平移得到。
C选项：$y = -\frac{1}{2}x^{2} + 2025x - 2024$，虽然$x$的系数发生了变化，但二次项系数仍为$-\frac{1}{2}$，在平移过程中，一次项系数和常数项可以变化，所以仍然可能通过平移得到。
D选项：$y = -x^{2} + x + 1$，二次项系数为$-1$，与原抛物线的二次项系数$-\frac{1}{2}$不同，因此不可能通过平移得到。
【答案】：
D

2.已知二次函数$y = ax^{2}+bx + c$中的部分$x,y$的对应值满足下表,则这个二次函数的表达式为(A)
|$x$|…|$0$|$2$|$3$|$4$|…|
|$y$|…|$1$|$-1$|$-0.5$|$1$|…|
A.$y = \frac{1}{2}x^{2}-2x + 1$
B.$y = -\frac{1}{2}x^{2}-2x + 1$
C.$y = \frac{1}{2}x^{2}+2x + 1$
D.$y = -\frac{1}{2}x^{2}+2x + 1$

答案： 解：将$x=0,y=1$代入$y=ax^{2}+bx + c$，得$c=1$。
将$x=2,y=-1$，$x=4,y=1$及$c=1$代入，得：
$\begin{cases}4a + 2b + 1=-1 \\16a + 4b + 1=1\end{cases}$
化简得：
$\begin{cases}4a + 2b=-2 \\16a + 4b=0 \end{cases}$
由第一个方程得$2a + b=-1$，即$b=-1 - 2a$。
将$b=-1 - 2a$代入第二个方程：$16a + 4(-1 - 2a)=0$，解得$a=\frac{1}{2}$。
则$b=-1 - 2×\frac{1}{2}=-2$。
所以二次函数表达式为$y=\frac{1}{2}x^{2}-2x + 1$。
答案：A

3.已知抛物线$y = -(x - m)^{2}+2m过不同的两点A(a,n),B(b,n)$,则当点$C(a + b,m)$在该抛物线上时,$m$的值为(C)
A.$0$
B.$1$
C.$0或1$
D.$\pm1$

答案： 解：
∵抛物线$y=-(x-m)^2+2m$过不同的两点$A(a,n)$，$B(b,n)$，
∴抛物线对称轴为直线$x=\frac{a+b}{2}$。
又
∵抛物线$y=-(x-m)^2+2m$的对称轴为直线$x=m$，
∴$\frac{a+b}{2}=m$，即$a+b=2m$。
∵点$C(a+b,m)$在该抛物线上，$a+b=2m$，
∴点$C$坐标为$(2m,m)$。
将$C(2m,m)$代入$y=-(x-m)^2+2m$，得：
$m=-(2m - m)^2 + 2m$
$m=-m^2 + 2m$
$m^2 - m = 0$
$m(m - 1)=0$
解得$m=0$或$m=1$。
当$m=0$时，抛物线为$y=-x^2$，此时$A$，$B$两点关于对称轴对称且不同，符合题意；
当$m=1$时，抛物线为$y=-(x - 1)^2 + 2$，此时$A$，$B$两点关于对称轴对称且不同，符合题意。
综上，$m$的值为$0$或$1$。
答案：C

4.已知二次函数的图象如图所示,则这个二次函数的表达式为$y=(x+1)^2-4$.

答案： 【解析】：
根据题目所给的二次函数图像，可知该函数是一个开口向上的抛物线，顶点在$(-1,-4)$，并且与$x$轴交于$(1,0)$和$(-3,0)$。
根据二次函数的顶点式$y=a(x-h)^2+k$，其中$(h,k)$是顶点坐标，可以设这个二次函数的表达式为$y=a(x+1)^2-4$。
利用已知的与$x$轴的交点$(1,0)$，代入上述表达式，得到方程$0=a(1+1)^2-4$。
解这个方程，可以得到$a$的值。
计算得$a=1$。
将$a$的值代入顶点式，得到二次函数的表达式。
【答案】：
$y=(x+1)^2-4$

5.一个二次函数,当自变量$x = 0$时,函数值$y = -1$;当$x = -2与\frac{1}{2}$时,$y = 0$,则这个二次函数的表达式为______$y = x^{2} + \frac{3}{2}x - 1$.

答案： 【解析】：
本题主要考查二次函数表达式的求解。根据题目条件，我们知道二次函数在$x=0$时，$y=-1$；在$x=-2$和$x=\frac{1}{2}$时，$y=0$。
我们可以设二次函数的表达式为$y=a(x+2)(x-\frac{1}{2})$，其中$a$是待求的系数。
然后我们将$x=0,y=-1$代入得到的表达式，可以求解出$a$的值。
最后我们将求得的$a$值代入原表达式，即可得到二次函数的表达式。
【答案】：
解：设二次函数的表达式为$y = a(x + 2)(x - \frac{1}{2})$。
由题意，当$x = 0$时，$y = - 1$，代入得：
$- 1 = a × 2 × ( - \frac{1}{2})$，
解得：$a = 1$。
因此，二次函数的表达式为：
$y = (x + 2)(x - \frac{1}{2}) = x^{2} + \frac{3}{2}x - 1$。
故答案为：$y = x^{2} + \frac{3}{2}x - 1$。

6.请写出一个图象的对称轴为$y$轴,开口向下,且经过点$(1,-2)$的二次函数表达式,这个二次函数的表达式可以是$y = -x^2 - 1$.

答案： 解：设二次函数表达式为$y = ax^2 + c$（$a \neq 0$）。
因为对称轴为$y$轴，所以表达式符合上述形式。
又因为开口向下，所以$a ＜ 0$。
函数经过点$(1, -2)$，代入得$a + c = -2$。
令$a = -1$，则$c = -1$。
所以二次函数表达式可以是$y = -x^2 - 1$。
$y = -x^2 - 1$

7.分别求下列函数的表达式:
(1)已知二次函数的图象经过点$A(1,0),B(3,0),C(0,3)$.
(2)已知某个二次函数图象的顶点的纵坐标为$2$,图象顶点在直线$y = x + 1$上,并且图象经过点$(3,-6)$.

答案： 【解析】：
本题主要考查二次函数表达式的确定，具体分为两个部分：
(1) 根据给定的三个点求二次函数的表达式；
(2) 根据二次函数的顶点坐标和另一个已知点求二次函数的表达式。
对于第一部分，我们可以设二次函数的表达式为$y = a(x - x_1)(x - x_2)$，其中$x_1$和$x_2$是二次函数与x轴的交点，然后通过代入点C的坐标来求解a。
对于第二部分，我们可以通过顶点的纵坐标和顶点在直线$y = x + 1$上的条件来求出顶点的横坐标，然后设二次函数的表达式为顶点式，再通过代入已知点来求解。
【答案】：
(1)
解：因为二次函数的图象经过点$A(1,0),B(3,0)$，所以可设二次函数的表达式为$y = a(x - 1)(x - 3)$。
又因为二次函数的图象经过点$C(0,3)$，代入得：
$3 = a(0 - 1)(0 - 3) = 3a$
解得：$a = 1$。
所以，二次函数的表达式为$y = (x - 1)(x - 3) = x^2 - 4x + 3$。
(2)
解：因为二次函数图象的顶点在直线$y = x + 1$上，且纵坐标为2，代入得顶点的横坐标为$x = 1$，所以顶点坐标为$(1,2)$。
设二次函数的表达式为$y = a(x - 1)^2 + 2$。
又因为二次函数的图象经过点$(3,-6)$，代入得：
$-6 = a(3 - 1)^2 + 2$
$-6 = 4a + 2$
解得：$a = -2$。
所以，二次函数的表达式为$y = -2(x - 1)^2 + 2 = -2x^2 + 4x$。

8.如图,抛物线$y = ax^{2}+bx - 5与x轴交于A(-1,0),B(5,0)$两点,与$y轴交于点C$,顶点为$D$.
(1)求此抛物线的表达式及顶点坐标.
(2)连结$BC,CD,BD$,求$\triangle BCD$的面积.

答案： 【解析】：
（1）本题考查的是利用待定系数法求二次函数解析式以及利用配方法求顶点坐标。
已知抛物线$y = ax^2 + bx - 5$与$x$轴交于$A(-1,0)$，$B(5,0)$两点，与$y$轴交于点$C$，顶点为$D$。
因为抛物线$y = ax^2 + bx - 5$经过$A(-1,0)$，$B(5,0)$两点，
所以，可得$\begin{cases}a-b-5=0,\\25a+5b-5=0.\end{cases}$
解得，$\begin{cases}a=1,\\b=-4.\end{cases}$
因此，该抛物线的表达式为$y = x^2 - 4x - 5$。
将抛物线表达式配方得：$y = x^2 - 4x - 5=(x-2)^2-9$，
因此，顶点$D$的坐标为$(2, -9)$。
（2）本题考查的是抛物线与$y$轴交点坐标以及三角形面积的计算。
过点$D$作$DE\perp x$轴于点$E$，交$BC$于点$F$
因为抛物线$y = x^2 - 4x - 5$与$y$轴交于点$C$，
所以，点$C$的坐标为$(0, -5)$。
设直线$BC$的解析式为$y = kx + c$，
那么，可得$\begin{cases}5k+c=0,\\c=-5.\end{cases}$
解得，$\begin{cases}k=1,\\c=-5.\end{cases}$
则直线$BC$的解析式为$y = x - 5$。
因为$DE\perp x$轴，点$D$的坐标为$(2, -9)$，
所以，点$E$的坐标为$(2, 0)$，点$F$的坐标为$(2, -3)$。
所以，$DE = 9$，$EF = 3$。
那么，$DF = DE - EF = 9 - 3 = 6$。
因为$B$的坐标为$(5, 0)$，点$E$的坐标为$(2, 0)$，
所以，$BE = 5 - 2 = 3$。
$S_{\triangle BCD}=S_{\triangle BDF}+S_{\triangle BDC}=\frac{1}{2} × BE × DF+\frac{1}{2} × BE × OC=\frac{1}{2} × 3 × 6+\frac{1}{2} × 3 × 5=15$。
【答案】：
(1)抛物线的表达式为$y = x^2 - 4x - 5$，顶点$D$的坐标为$(2, -9)$；
(2)$\triangle BCD$的面积为$15$。