3. 如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度。现采取以下措施:在地面选取一点C,测得∠BCA= 45°,AC= 20米,∠BAC= 60°,则这棵乌稔树的高AB约为
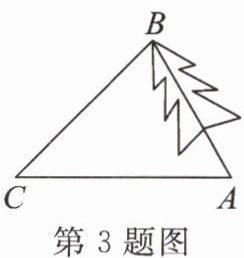
14
米(结果精确到1米,参考数据:√2≈1.4,√3≈1.7)。
答案:
14
4. 在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图所示),那么,由此可知,B、C两地相距
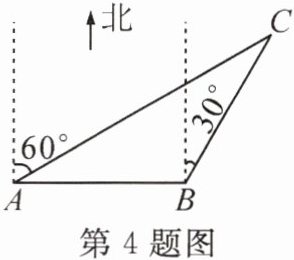
200
m。
答案:
200
5. 东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应。如图所示,城门楼B在角楼A的正东方向520m处,南关桥C在城门楼B的正南方向1200m处。在明珠大剧院P测得角楼A在北偏东68.2°方向,南关桥C在南偏东56.31°方向(点A,B,C,P四点在同一平面内),求明珠大剧院到龙堤BC的距离(结果精确到1m,参考数据:sin68.2°≈0.928,cos68.2°≈0.371,tan68.2°≈2.50,sin56.31°≈0.832,cos56.31°≈0.555,tan56.31°≈1.50)。
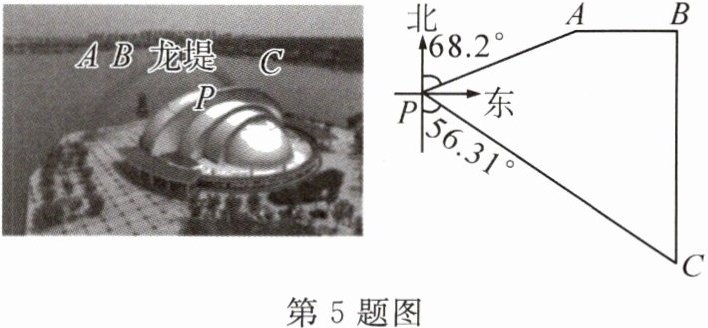

答案:
解:如图,过点P作PE⊥BC于点E,过点A作AD⊥PE 于点D,则四边形ADEB是矩形,
∴DE=AB=520m,设PD=xm,在Rt△APD中,
∵∠PAD=68.2°,
∴AD = PD/tan68.2°≈x/2.5m,
∴BE=AD≈x/2.5m,
∴PE=PD + DE=(x + 520)m,CE=BC - BE≈(1200 - 2x/5)m,在Rt△PCE 中,tanC=tan56.31°=PE/CE≈(x + 520)/(1200 - 2x/5)≈1.5,解得x≈800,
∴PD≈800m,
∴PE=PD + DE≈800 + 520 = 1320(m).答:明珠大剧院到龙堤BC的距离约为1320m.
∴DE=AB=520m,设PD=xm,在Rt△APD中,
∵∠PAD=68.2°,
∴AD = PD/tan68.2°≈x/2.5m,
∴BE=AD≈x/2.5m,
∴PE=PD + DE=(x + 520)m,CE=BC - BE≈(1200 - 2x/5)m,在Rt△PCE 中,tanC=tan56.31°=PE/CE≈(x + 520)/(1200 - 2x/5)≈1.5,解得x≈800,
∴PD≈800m,
∴PE=PD + DE≈800 + 520 = 1320(m).答:明珠大剧院到龙堤BC的距离约为1320m.
6. 教育部颁布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动。如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i= 1:2.4,AB= 13米,AE= 29米。
(1)求点B距水平地面AE的高度。
(2)若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由(测角器的高度忽略不计,结果精确到0.1米,参考数据sin53°≈4/5,cos53°≈3/5,tan53°≈4/3)。
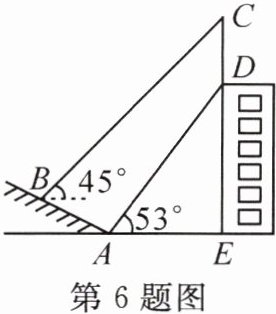
(1)求点B距水平地面AE的高度。
(2)若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由(测角器的高度忽略不计,结果精确到0.1米,参考数据sin53°≈4/5,cos53°≈3/5,tan53°≈4/3)。

答案:
解:
(1)如图,过点B作BM⊥AE于点M,由题意可知,i = 1:2.4 = 5/12 = BM/AM,设BM=5x米,AM=12x米,则AB = √((5x)² + (12x)²)=13x(米),
∴13x=13,解得x=1,
∴BM=5米,AM=12米,即点B 距水平地面AE的高度为5米.
(2)如图,作BN⊥CE于点N,
∵BM⊥AE,CE⊥AE,
∴四边形BMEN是矩形.
∴NE=BM=5米,BN=ME=12 + 29 = 41(米).在Rt△BCN中,∠CBN=45°,
∴CN=BN=41米,CE = 41 + 5 = 46(米).在Rt△ADE中,∠DAE=53°,AE = 29米,
∴DE=AE × tan53°≈29 × 4/3 = 116/3(米),
∴CD=CE - DE=46 - 116/3 = 22/3(米),
∵22/3>7,
∴该公司的广告牌不符合要求.
(1)如图,过点B作BM⊥AE于点M,由题意可知,i = 1:2.4 = 5/12 = BM/AM,设BM=5x米,AM=12x米,则AB = √((5x)² + (12x)²)=13x(米),
∴13x=13,解得x=1,
∴BM=5米,AM=12米,即点B 距水平地面AE的高度为5米.
(2)如图,作BN⊥CE于点N,
∵BM⊥AE,CE⊥AE,
∴四边形BMEN是矩形.
∴NE=BM=5米,BN=ME=12 + 29 = 41(米).在Rt△BCN中,∠CBN=45°,
∴CN=BN=41米,CE = 41 + 5 = 46(米).在Rt△ADE中,∠DAE=53°,AE = 29米,
∴DE=AE × tan53°≈29 × 4/3 = 116/3(米),
∴CD=CE - DE=46 - 116/3 = 22/3(米),
∵22/3>7,
∴该公司的广告牌不符合要求.
查看更多完整答案,请扫码查看


