《2025年名师金典九年级数学全一册浙教版》

9. 如图,$∠AOB= 2∠COD$,则下列结论中成立的是(B)

A.$\widehat {AB}＞2\widehat {CD}$
B.$\widehat {AB}= 2\widehat {CD}$
C.$\widehat {AB}＜2\widehat {CD}$
D.不能确定$\widehat {AB}与2\widehat {CD}$的大小关系

答案： B

10. 如图,半径为$5的\odot A$中,弦$BC$,$ED所对的圆心角分别是∠BAC$,$∠EAD$,已知$DE= 6$,$∠BAC+∠EAD= 180^{\circ }$,则圆心$A到弦BC$的距离等于____3.

答案： 3

11. 如图,已知在$\odot O$中,弦$AB与半径OE$,$OF交于点C$,$D$,$AC= BD$,求证：
(1)$OC= OD$.
(2)$\widehat {AE}= \widehat {BF}$.

答案： 证明:
(1)如图，连结OA，OB.
∵OA = OB，
∴∠OAC = ∠OBD.在△OAC与△OBD中，$\left\{\begin{array}{l}OA = OB,\\ \angle OAC = \angle OBD,\\ AC = BD,\end{array}\right.$
∴△OAC≌△OBD(SAS).
∴OC = OD.
(2)
∵△OAC≌△OBD，
∴∠AOC = ∠BOD，
∴$\overset{\frown}{AE}=\overset{\frown}{BF}$.

12. 如图,在$\odot O$中,$AB$,$DE为\odot O$的直径,$C是\odot O$上一点,且$\widehat {AD}= \widehat {CE}$.
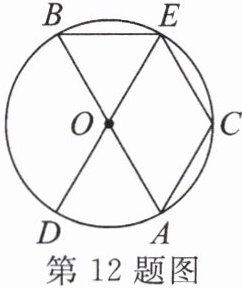
(1)$\widehat {BE}与\widehat {CE}$有什么数量关系？为什么？
(2)若$∠BOE= 60^{\circ }$,则四边形$OACE$是什么特殊的四边形？请说明理由.

答案： 解:
(1)$\overset{\frown}{BE}=\overset{\frown}{CE}$.理由:
∵AB，DE是⊙O的直径，
∴∠AOD = ∠BOE，
∴$\overset{\frown}{AD}=\overset{\frown}{BE}$.
∵$\overset{\frown}{AD}=\overset{\frown}{CE}$，
∴$\overset{\frown}{BE}=\overset{\frown}{CE}$.
(2)四边形OACE是菱形.理由:连结OC，如图.
∵∠BOE = 60°，$\overset{\frown}{BE}=\overset{\frown}{CE}$，
∴∠COE = 60°.
∵OC = OE，
∴△COE是等边三角形.
∵∠AOC = 180° - 60° - 60° = 60°，OA = OC，
∴△AOC是等边三角形，
∴OE = CE = OA = AC = OC，
∴四边形OACE是菱形.

13. 如图,过$\odot O的直径AB上两点M$,$N$,分别作弦$CD$,$EF$,$CD// EF$,$AC= BF$.求证：
(1)$\widehat {BC}= \widehat {AF}$.
(2)$AM= BN$.

答案： 证明:
(1)如图，连结OC，OF，则OC = OA = OB = OF.又
∵AC = BF，
∴△AOC≌△BOF(SSS)，
∴∠COA = ∠BOF，
∴∠COB = ∠FOA.
∴$\overset{\frown}{BC}=\overset{\frown}{AF}$.
(2)
∵∠COA = ∠BOF，OC = OF = OA = OB，
∴∠CAB = ∠OCA = ∠BFO = ∠ABF.
∵CD//EF，
∴∠AMC = ∠ANE；又
∵∠BNF = ∠ANE，
∴∠AMC = ∠BNF.在△AMC和△BNF中，$\left\{\begin{array}{l}\angle AMC = \angle BNF,\\ \angle CAB = \angle ABF,\\ AC = BF,\end{array}\right.$
∴△AMC≌△BNF(AAS)，
∴AM = BN.