《2025年名师金典九年级数学全一册浙教版》

1. 如图所示的圆中,下列各角是圆心角的是(B)
A.$∠ABC$
B.$∠AOB$
C.$∠OAB$
D.$∠OCB$

答案： B

2. 如图,$AB是\odot O$的直径.若$∠AOC= 70^{\circ }$,且$AD// OC$,则$\widehat {AD}$的度数为(D)
A.$70^{\circ }$
B.$60^{\circ }$
C.$50^{\circ }$
D.$40^{\circ }$

答案： D

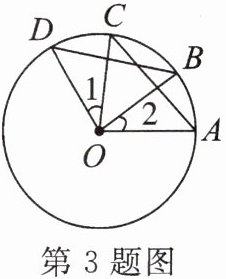
3. 如图,$A$,$B$,$C$,$D是\odot O$上的点,$∠1= ∠2$,给出下列结论：①$\widehat {AB}= \widehat {CD}$；②$\widehat {BD}= \widehat {AC}$；③$AC= BD$；④$∠BOD= ∠AOC$.其中正确的有(D)

A.1个
B.2个
C.3个
D.4个

答案： D

4. 一条弦把圆分成$1:5$两部分,则这条弦所对的圆心角的度数是60°.

答案： 60°

5. 如图,半圆$O$是一个量角器,$\triangle AOB$为一纸片,$AB交半圆于点D$,$OB交半圆于点C$.若点$C$,$D$,$A在量角器上对应读数分别为45^{\circ }$,$70^{\circ }$,$150^{\circ }$,则$∠AOB$的度数为105°,$∠A$的度数为50°.

答案： 105° 50°

6. 如图,点$A$,$B$,$C在半径为4的\odot O$上,$D$,$E分别是弦AB$,$BC$的中点,连结$DE$.若弧$AB的度数为70^{\circ }$,弧$BC的度数为50^{\circ }$,则$DE$的长度为$2\sqrt{3}$.

答案： $2\sqrt{3}$

7. 如图,在$\triangle ABC$中,$∠B= 90^{\circ }$,$∠C= 30^{\circ }$.以$B$为圆心,$AB$为半径作圆,交$AC于点D$,交$BC于点E$.
(1)求$\widehat {ED}$的度数.
(2)求证：$D是AC$的中点.

答案：
(1)解:如图，连结BD.
∵在△ABC中，∠ABC = 90°，∠C = 30°，
∴∠A = 60°.
∵BA = BD，
∴△ABD是等边三角形，
∴∠ABD = 60°，
∴∠DBE = ∠ABC - ∠ABD = 30°，
∴$\overset{\frown}{ED}$的度数为30°.
(2)证明:由
(1)得△ABD为等边三角形，
∴DB = AD.
∵∠DBC = ∠C = 30°，
∴DC = DB，
∴DC = AD，即D为AC的中点.

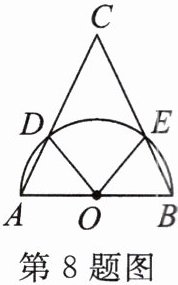
8. 如图,$O为等腰三角形ABC的底边AB$的中点,以点$O$为圆心,$AB为直径的半圆分别交AC$,$BC于点D$,$E$.
(1)求证：$∠AOE= ∠BOD$.
(2)求证：$\widehat {AD}= \widehat {BE}$.

答案： 证明:
(1)
∵CA = CB，
∴∠A = ∠B.
∵OA = OD，OB = OE，
∴∠A = ∠ODA，∠B = ∠OEB，
∴∠AOD = ∠BOE，
∴∠AOD + ∠DOE = ∠BOE + ∠DOE，
∴∠AOE = ∠BOD.
(2)
∵∠AOD = ∠BOE，
∴$\overset{\frown}{AD}=\overset{\frown}{BE}$.