《2025年名师金典九年级数学全一册浙教版》

1. 经过$\odot O的直径的一端能作\odot O$的切线 (B)
A.0条
B.1条
C.2条
D.3条

答案： B

2. 下列直线中,一定是圆的切线的是 (C)
A.与圆有公共点的直线
B.垂直于圆的半径的直线
C.与圆心的距离等于半径的直线
D.经过圆的直径一端的直线

答案： C

3. 如图,$\triangle ABC是\odot O$的内接三角形,下列选项中,能使过点A的直线EF与$\odot O$相切于点A的条件是 (A)

A.$∠EAB= ∠C$
B.$∠B= 90^{\circ }$
C.$EF⊥AC$
D.AC是$\odot O$的直径

答案： A

4. 在平面直角坐标系中,以点$(2,1)$为圆心,1为半径的圆必与x轴相切.

答案： x

5. 如图,$\triangle ABC$的一边AB是$\odot O$的直径,请你添加一个条件,使BC是$\odot O$的切线,你所添加的条件为∠ABC=90°(答案不唯一).

答案： ∠ABC=90°(答案不唯一)

6. 如图,$\odot O$的半径为4 cm,BC是直径,若$AB= 10cm$,则当$AC= $6cm时,AC是$\odot O$的切线.

答案： 6

7. 如图,$\triangle ABC$为等腰三角形,$AB= AC$,O是底边BC的中点,$\odot O$与腰AB相切于点D,求证：AC与$\odot O$相切.

答案：
证明:如图，连结OD,过点O作OE⊥AC于E点,则∠OEC=90°.
∵AB与⊙O相切于点D,
∴OD⊥AB,
∴∠ODB=90°,
∴∠ODB=∠OEC;又
∵O是BC的中点，
∴OB=OC,
∵AB=AC,
∴∠B=∠C,
∴△OBD≌△OCE,
∴OE=OD,即OE是⊙O的半径，
∴AC与⊙O相切.

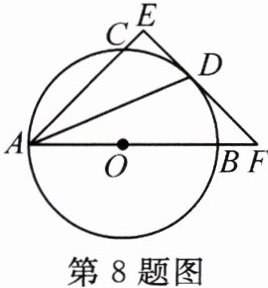
8. 如图,AB是$\odot O$的直径,点C,D在$\odot O$上,且AD平分$∠CAB$. 过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F. 求证：EF与$\odot O$相切.

答案：
证明:如图，连结OD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠FOD=2∠BAD,AD平分∠CAB,
∴∠EAF=2∠BAD,
∴∠EAF=∠FOD,
∵AE⊥EF,
∴∠AEF=90°,
∴∠EAF+∠EFA=90°,
∴∠DFO+∠DOF=90°,
∴∠ODF=90°,
∴OD⊥EF,即EF与⊙O相切.