《2025年名师金典九年级数学全一册浙教版》

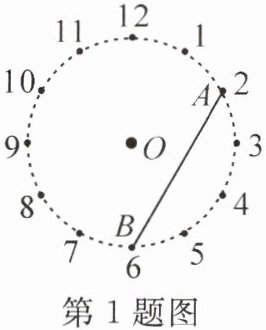
1. 如图是用$\odot O$制作的表盘模型,其中点A,B分别与整钟点“2时”,“6时”重合,要使$∠ABC= 90^{\circ }$,则点C应位于(B)

A.“7时”处
B.“8时”处
C.“9时”处
D.“10时”处

答案： B

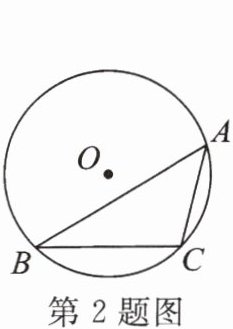
2. 如图,$\odot O为△ABC$的外接圆,$∠A= 45^{\circ }$,$\odot O$的半径为2,则BC的长为(B)

A.2
B.$2\sqrt {2}$
C.4
D.$2\sqrt {3}$

答案： B

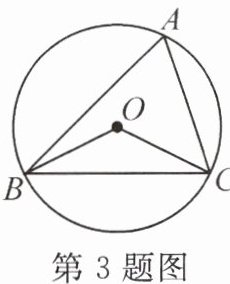
3. 有一题目：“已知点O为$△ABC$的外心,$∠BOC= 130^{\circ }$,求$∠A$.”嘉嘉的解答为：画$△ABC以及它的外接圆\odot O$,连结OB,OC,如图,由$∠BOC= 2∠A= 130^{\circ }$,得$∠A= 65^{\circ }$.而淇淇说：“嘉嘉考虑得不周全,还应有另一个不同的值.”下列判断正确的是(A)

A.淇淇说的对,且$∠A的另一个值是115^{\circ }$
B.淇淇说的不对,$∠A就得65^{\circ }$
C.嘉嘉求的结果不对,$∠A应得50^{\circ }$
D.两人都不对,应有3个不同的值

答案： A

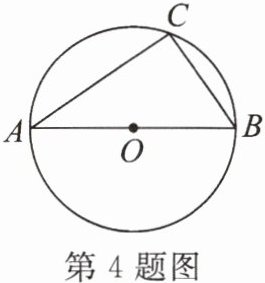
4. 如图,AB是$\odot O$的直径,点C在$\odot O$上,$∠A= 35^{\circ }$,则$∠B= $55$^{\circ }$.

答案： 55

5. 如图,AB是$\odot O$的直径,C,D是$\odot O$上两点,BA平分$∠CBD$.若$∠AOD= 50^{\circ }$,则$∠A$的度数为______65°.

答案： 65°

6. 如图,AD是$\odot O$的直径,将弧AB沿弦AB折叠后,弧AB刚好经过圆心O.若$BD= 6$,则$\odot O$的半径是______6.

答案： 6

7. 如图,在$\odot O$中,弦CD与直径AB相交于点P.
(1)若$∠ABC= 62^{\circ }$,$∠APC= 100^{\circ }$,则$∠BAD=$38$^{\circ }$,$∠CDB=$28$^{\circ }$.
(2)若$\overset{\frown }{AD}$的度数为m,$\overset{\frown }{BC}$的度数为n,猜想：$∠APD$的度数与m,n之间的数量关系,并证明你的结论.
解:∠APD=$\frac{1}{2}$(m+n). 证明:
∵$\overset{\frown}{AD}$的度数为m,$\overset{\frown}{BC}$的度数为n,
∴∠ABD=$\frac{1}{2}$m,∠CDB=$\frac{1}{2}$n.
∵∠APD=∠ABD+∠CDB,
∴∠APD=$\frac{1}{2}$(m+n).

答案：
(1)38　28
(2)解:∠APD=$\frac{1}{2}$(m+n). 证明:
∵$\overset{\frown}{AD}$的度数为m,$\overset{\frown}{BC}$的度数为n,
∴∠ABD=$\frac{1}{2}$m,∠CDB=$\frac{1}{2}$n.
∵∠APD=∠ABD+∠CDB,
∴∠APD=$\frac{1}{2}$(m+n).

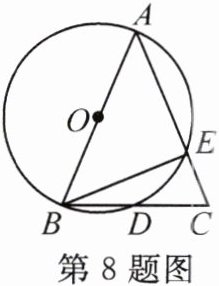
8. 如图,在$△ABC$中,$AB= AC$,$∠BAC= 45^{\circ }$,以AB为直径的$\odot O$交BC于点D,交AC于点E.
(1)求$∠EBC$的度数.
(2)求证：$BD= CD$.

答案：
(1)解:
∵AB是⊙O的直径，
∴∠AEB =90°.又
∵∠BAC=45°,
∴∠ABE=45°.又
∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=∠ABC−∠ABE=22.5°.
(2)证明:如图，连结AD.
∵AB是⊙O 的直径，
∴∠ADB=90°.
∴AD⊥BC;又
∵AB=AC,
∴BD=CD.