《2025年名师金典九年级数学全一册浙教版》

9. 高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面宽AB= 8米,C是圆弧上一点,且$\overset{\frown}{AC}= \overset{\frown}{BC}$,连结CO并延长交AB于点D,CD= 8米,则此圆的半径OA= (A)
A.5米
B.$\frac{11}{2}$米
C.6米
D.$\frac{13}{2}$米

答案： A

10. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为$2\sqrt{3}$。

答案： $2\sqrt{3}$

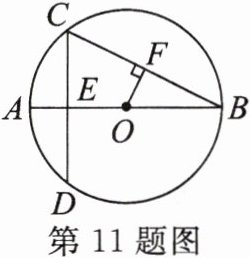
11. 如图,AB是⊙O的直径且交弦CD于点E,弧AC= 弧AD,AE= 2,CD= 8。
(1)求⊙O的半径。
(2)连结BC,作OF⊥BC于点F,求OF的长。

答案： 解:
(1)连结OD,如图.设$\odot O$的半径为r.
∵弧AC=弧AD,AB是直径,
∴AB⊥CD,
∴∠OED=90°,DE=CE=$\frac{1}{2}$CD=$\frac{1}{2}$×8=4.在Rt△ODE中,
∵OE=r−2,OD=r,DE=4,
∴(r−2)²+4²=r²,解得r=5,即$\odot O$的半径为5.
(2)在Rt△BCE中,
∵CE=4,BE=AB−AE=8,
∴BC=$\sqrt{4^{2}+8^{2}}=4\sqrt{5}$.
∵OF⊥BC,
∴BF=CF=$\frac{1}{2}$BC=$2\sqrt{5}$,∠OFB=90°.在Rt△OBF中，OF=$\sqrt{BO^{2}-BF^{2}}=\sqrt{5^{2}-(2\sqrt{5})^{2}}=\sqrt{5}$,即OF的长为$\sqrt{5}$.

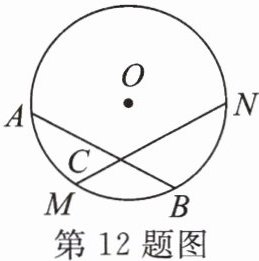
12. 如图,M是$\overset{\frown}{AB}$的中点,过点M的弦MN交弦AB于点C,⊙O的半径为4,MN= $4\sqrt{3}$。
(1)求圆心O到弦MN的距离。
(2)求∠ACM的度数。

答案： 解:
(1)如图，连结OM,过点O作OD⊥MN于点D.由垂径定理，得MD=$\frac{1}{2}$MN=$2\sqrt{3}$.在Rt△ODM中,OM=4,MD=$2\sqrt{3}$,
∴OD=$\sqrt{OM^{2}-MD^{2}}=2$.故圆心O到弦MN的距离为2.
(2)在Rt△ODM中,OM=4,OD=2,
∴∠OMD=30°.
∵M是$\widehat{AB}$的中点,
∴OM⊥AB,
∴∠ACM=90°−30°=60°.

13. 如图,某地欲搭建一座圆弧型拱桥,跨度AB= 32米,拱高CD= 8米(C为AB的中点,D为弧AB的中点)。
(1)求该圆弧所在圆的半径。
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度。

答案： 解:
(1)如图，设弧AB所在圆的圆心为O,C为AB的中点，D为弧AB的中点，则CD⊥AB于点C,CB=$\frac{AB}{2}=\frac{32}{2}=16$(米),延长DC经过点O.设$\odot O$的半径为R米.在Rt△OBC中,OB²=OC²+CB²,
∴R²=(R−8)²+16²,解得R=20,则$\odot O$的半径为20米.
(2)过点O作OH⊥FE交FE的延长线于点H,如图,则OH=CE=16−4=12(米),OF=R=20米,在Rt△OHF中,HF=$\sqrt{20^{2}-12^{2}}=16$(米).
∵HE=OC =OD−CD=20−8=12(米),
∴EF=HF−HE=16−12 =4(米),
∴桥墩的高度为4米.