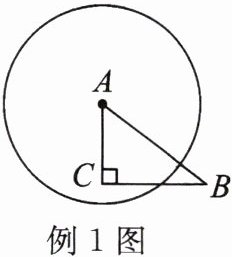
例1 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AB= 5$,$BC= 4$.以点$A$为圆心,$r$为半径作圆,当点$C在\odot A内且点B在\odot A$外时,$r$的值可能是(
A.3
B.4
C.5
D.6
B
)
A.3
B.4
C.5
D.6
答案:
【解析】:本题主要考查点与圆的位置关系。
在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AB= 5$,$BC= 4$,
根据勾股定理可得:
$AC=\sqrt{AB^2-BC^2}=\sqrt{5^2-4^2}=3$,
因为点$C$在$\odot A$内,点$B$在$\odot A$外,
所以$AC<r<AB$,
即$3<r<5$,
在给定的选项中,只有$r=4$满足这个条件。
【答案】:B
在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AB= 5$,$BC= 4$,
根据勾股定理可得:
$AC=\sqrt{AB^2-BC^2}=\sqrt{5^2-4^2}=3$,
因为点$C$在$\odot A$内,点$B$在$\odot A$外,
所以$AC<r<AB$,
即$3<r<5$,
在给定的选项中,只有$r=4$满足这个条件。
【答案】:B
变式1-1 在$\odot O$中,半径为5,圆心$O$在坐标原点上,点$P的坐标为(3,4)$,则点$P与\odot O$的位置关系是(
A.点$P在\odot O$内
B.点$P在\odot O$上
C.点$P在\odot O$外
D.不能确定
B
)A.点$P在\odot O$内
B.点$P在\odot O$上
C.点$P在\odot O$外
D.不能确定
答案:
【解析】:
首先,我们需要知道点与圆的位置关系可以通过比较点到圆心的距离与圆的半径来确定。
点到圆心的距离公式为:$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$,其中$(x_1, y_1)$是圆心的坐标,$(x_2, y_2)$是点的坐标。
在本题中,圆心$O$的坐标是$(0,0)$,点$P$的坐标是$(3,4)$。
代入公式,我们可以计算出点$P$到圆心$O$的距离:
$d = \sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$
由于计算出的距离$d$等于圆的半径$5$,所以我们可以判断点$P$在圆上。
【答案】:
B. 点$P$在$\odot O$上。
首先,我们需要知道点与圆的位置关系可以通过比较点到圆心的距离与圆的半径来确定。
点到圆心的距离公式为:$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$,其中$(x_1, y_1)$是圆心的坐标,$(x_2, y_2)$是点的坐标。
在本题中,圆心$O$的坐标是$(0,0)$,点$P$的坐标是$(3,4)$。
代入公式,我们可以计算出点$P$到圆心$O$的距离:
$d = \sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$
由于计算出的距离$d$等于圆的半径$5$,所以我们可以判断点$P$在圆上。
【答案】:
B. 点$P$在$\odot O$上。
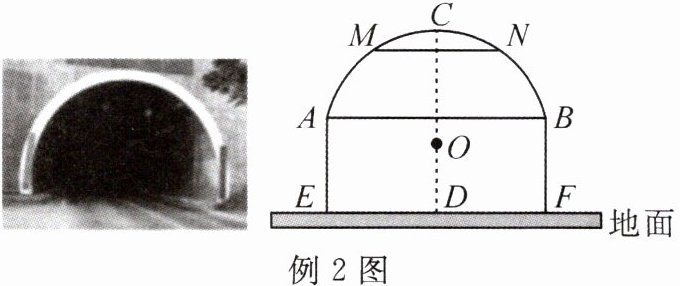
例2 某公路上有一隧道,如图,隧道顶部是圆弧形拱顶,圆心为$O$,隧道的水平宽$AB$为24m,$AB离地面的高度AE= 10m$,拱顶最高处$C离地面的高度CD= 18m$,在拱顶的$M$,$N$处安装照明灯,且$M$,$N$离地面的高度相等且都等于17m,求$MN$的长.

答案:
解:设圆弧形拱顶半径为$r$m,圆心$O$到地面距离为$h$m。
由题意得:$CD = 18$m,$AE = BF = 10$m,$AB = 24$m,$OD\perp AB$于$D$,则$AD = \frac{AB}{2}=12$m。
$OC = r$,$CD = 18$m,故$OD = CD - OC = 18 - r$,则$h = OD = 18 - r$。
$OA = r$,$AE = 10$m,$OE = h = 18 - r$,$AE\perp EF$,$OD\perp EF$,$AD = 12$m,在$Rt\triangle AOD$中:$OA^2 = AD^2 + OD^2$,即$r^2 = 12^2 + (18 - r)^2$。
展开得:$r^2 = 144 + 324 - 36r + r^2$,化简得$36r = 468$,解得$r = 13$。
$h = 18 - r = 5$m,即$OD = 5$m。
设$M$,$N$离地面高度为$17$m,过$M$作$MG\perp EF$于$G$,则$MG = 17$m,$OG = MG - h = 17 - 5 = 12$m。
连接$OM = r = 13$m,在$Rt\triangle OMG$中:$MG'^2 + OG^2 = OM^2$($G'$为$MN$与$OD$交点),$MG' = \sqrt{OM^2 - OG^2} = \sqrt{13^2 - 12^2} = 5$m。
$MN = 2MG' = 10$m。
答:$MN$的长为$10$m。
由题意得:$CD = 18$m,$AE = BF = 10$m,$AB = 24$m,$OD\perp AB$于$D$,则$AD = \frac{AB}{2}=12$m。
$OC = r$,$CD = 18$m,故$OD = CD - OC = 18 - r$,则$h = OD = 18 - r$。
$OA = r$,$AE = 10$m,$OE = h = 18 - r$,$AE\perp EF$,$OD\perp EF$,$AD = 12$m,在$Rt\triangle AOD$中:$OA^2 = AD^2 + OD^2$,即$r^2 = 12^2 + (18 - r)^2$。
展开得:$r^2 = 144 + 324 - 36r + r^2$,化简得$36r = 468$,解得$r = 13$。
$h = 18 - r = 5$m,即$OD = 5$m。
设$M$,$N$离地面高度为$17$m,过$M$作$MG\perp EF$于$G$,则$MG = 17$m,$OG = MG - h = 17 - 5 = 12$m。
连接$OM = r = 13$m,在$Rt\triangle OMG$中:$MG'^2 + OG^2 = OM^2$($G'$为$MN$与$OD$交点),$MG' = \sqrt{OM^2 - OG^2} = \sqrt{13^2 - 12^2} = 5$m。
$MN = 2MG' = 10$m。
答:$MN$的长为$10$m。
变式2-1 如图,在$\odot O$中,弦$AB// CD$,$OP\perp CD交\odot O于点P$,交$AB于点M$,交$CD于点N$,$OM= MN$,$AB= 18$,$CD= 12$,则$\odot O$的半径为(
A.4
B.$4\sqrt{2}$
C.$4\sqrt{6}$
D.$4\sqrt{3}$
C
)A.4
B.$4\sqrt{2}$
C.$4\sqrt{6}$
D.$4\sqrt{3}$
答案:
解:设$OM = x$,则$MN = x$,$ON = OM + MN = 2x$。
连接$OA$,$OC$。
因为$OP \perp CD$,$AB // CD$,所以$OP \perp AB$。
由垂径定理得:$AM = \frac{1}{2}AB = 9$,$CN = \frac{1}{2}CD = 6$。
在$Rt\triangle OMA$中,$OA^2 = OM^2 + AM^2 = x^2 + 9^2$。
在$Rt\triangle ONC$中,$OC^2 = ON^2 + CN^2 = (2x)^2 + 6^2$。
因为$OA = OC$(均为半径),所以$x^2 + 81 = 4x^2 + 36$。
解得$x^2 = 15$。
则半径$OA = \sqrt{x^2 + 81} = \sqrt{15 + 81} = \sqrt{96} = 4\sqrt{6}$。
答案:C
连接$OA$,$OC$。
因为$OP \perp CD$,$AB // CD$,所以$OP \perp AB$。
由垂径定理得:$AM = \frac{1}{2}AB = 9$,$CN = \frac{1}{2}CD = 6$。
在$Rt\triangle OMA$中,$OA^2 = OM^2 + AM^2 = x^2 + 9^2$。
在$Rt\triangle ONC$中,$OC^2 = ON^2 + CN^2 = (2x)^2 + 6^2$。
因为$OA = OC$(均为半径),所以$x^2 + 81 = 4x^2 + 36$。
解得$x^2 = 15$。
则半径$OA = \sqrt{x^2 + 81} = \sqrt{15 + 81} = \sqrt{96} = 4\sqrt{6}$。
答案:C
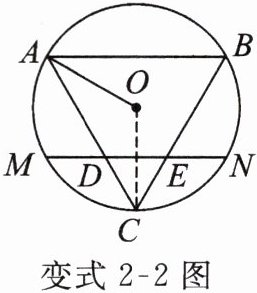
变式2-2 如图,在$\triangle ABC$中,$AC= BC= 5$,$AB= 6$,$D为AC$上一点,作$DE// AB交BC于点E$,点$C关于DE的对称点为点O$,以$OA为半径作\odot O恰好经过点C$,并交直线$DE于点M$,$N$,则$MN$的长为______
$\frac{25\sqrt{3}}{8}$
.
答案:
解:过点C作CH⊥AB于H,交DE于G。
∵AC=BC=5,AB=6,
∴AH=HB=3,CH=$\sqrt{AC^2 - AH^2}$=$\sqrt{5^2 - 3^2}$=4。
设CG=x,
∵DE//AB,
∴$\frac{CG}{CH}$=$\frac{CD}{CA}$,即$\frac{x}{4}$=$\frac{CD}{5}$,CD=$\frac{5x}{4}$。
∵点C与O关于DE对称,
∴OG=CG=x,OC=2x。
∵⊙O过点C,
∴OA=OC=2x。
在Rt△AOH中,OH=CH - OC=4 - 2x,AH=3,OA=2x,
由勾股定理得:$3^2 + (4 - 2x)^2 = (2x)^2$,
解得x=$\frac{25}{16}$,
∴OC=2x=$\frac{25}{8}$,OG=x=$\frac{25}{16}$。
在Rt△OMG中,OM=OA=$\frac{25}{8}$,OG=$\frac{25}{16}$,
MG=$\sqrt{OM^2 - OG^2}$=$\sqrt{(\frac{25}{8})^2 - (\frac{25}{16})^2}$=$\frac{25\sqrt{3}}{16}$,
∴MN=2MG=$\frac{25\sqrt{3}}{8}$。
$\frac{25\sqrt{3}}{8}$
∵AC=BC=5,AB=6,
∴AH=HB=3,CH=$\sqrt{AC^2 - AH^2}$=$\sqrt{5^2 - 3^2}$=4。
设CG=x,
∵DE//AB,
∴$\frac{CG}{CH}$=$\frac{CD}{CA}$,即$\frac{x}{4}$=$\frac{CD}{5}$,CD=$\frac{5x}{4}$。
∵点C与O关于DE对称,
∴OG=CG=x,OC=2x。
∵⊙O过点C,
∴OA=OC=2x。
在Rt△AOH中,OH=CH - OC=4 - 2x,AH=3,OA=2x,
由勾股定理得:$3^2 + (4 - 2x)^2 = (2x)^2$,
解得x=$\frac{25}{16}$,
∴OC=2x=$\frac{25}{8}$,OG=x=$\frac{25}{16}$。
在Rt△OMG中,OM=OA=$\frac{25}{8}$,OG=$\frac{25}{16}$,
MG=$\sqrt{OM^2 - OG^2}$=$\sqrt{(\frac{25}{8})^2 - (\frac{25}{16})^2}$=$\frac{25\sqrt{3}}{16}$,
∴MN=2MG=$\frac{25\sqrt{3}}{8}$。
$\frac{25\sqrt{3}}{8}$
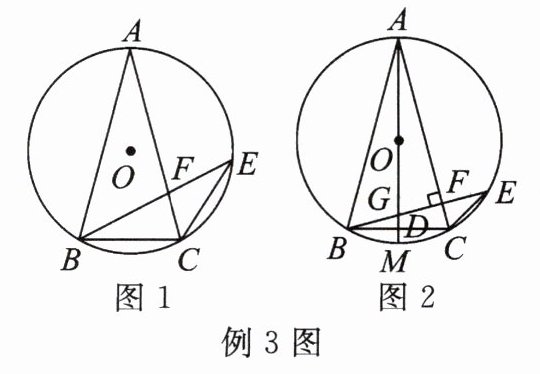
例3 如图1,在$\odot O$中,$AB= AC$,$\angle ACB= 75^{\circ}$,点$E在劣弧AC$上运动,连结$EC$,$BE$,交$AC于点F$.
(1)求$\angle E$的度数.
(2)当点$E运动到使BE\perp AC$时,如图2,连结$AO$并延长,交$BE于点G$,交$BC于点D$,交$\odot O于点M$.求证:$D为GM$的中点.
(1)求$\angle E$的度数.
(2)当点$E运动到使BE\perp AC$时,如图2,连结$AO$并延长,交$BE于点G$,交$BC于点D$,交$\odot O于点M$.求证:$D为GM$的中点.

答案:
(1)解:
∵AB=AC,
∴∠ABC=∠ACB=75°,
∴∠BAC=180°-75°×2=30°,
∵∠E与∠BAC所对弧为$\overset{\frown}{BC}$,
∴∠E=∠BAC=30°。
(2)证明:
∵AB=AC,AM为直径,
∴AM⊥BC,BD=CD,∠ABM=90°,
∵BE⊥AC,∠BAC=30°,设AF=2x,则BF=AF·tan30°=$\frac{2\sqrt{3}}{3}x$,AB=2BF=$\frac{4\sqrt{3}}{3}x$,在Rt△ABM中,∠BAM=15°,BM=AB·sin15°,AM=AB·cos15°,在Rt△BDG中,∠DBG=15°,BD=BC/2=AB·cos75°,DG=BD·tan15°,GM=AM - AG,AG=AF/cos15°=2x/cos15°,经计算DG=GM,即D为GM的中点。
(1)解:
∵AB=AC,
∴∠ABC=∠ACB=75°,
∴∠BAC=180°-75°×2=30°,
∵∠E与∠BAC所对弧为$\overset{\frown}{BC}$,
∴∠E=∠BAC=30°。
(2)证明:
∵AB=AC,AM为直径,
∴AM⊥BC,BD=CD,∠ABM=90°,
∵BE⊥AC,∠BAC=30°,设AF=2x,则BF=AF·tan30°=$\frac{2\sqrt{3}}{3}x$,AB=2BF=$\frac{4\sqrt{3}}{3}x$,在Rt△ABM中,∠BAM=15°,BM=AB·sin15°,AM=AB·cos15°,在Rt△BDG中,∠DBG=15°,BD=BC/2=AB·cos75°,DG=BD·tan15°,GM=AM - AG,AG=AF/cos15°=2x/cos15°,经计算DG=GM,即D为GM的中点。
变式3-1 如图,$OA$,$OB$,$OC都是\odot O$的半径,$\angle ACB= 2\angle BAC$.
(1)求证:$\angle AOB= 2\angle BOC$.
(2)若$AB= 4$,$BC= \sqrt{5}$,求$\odot O$的半径.
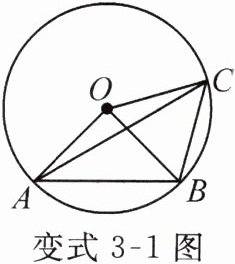
(1)求证:$\angle AOB= 2\angle BOC$.
(2)若$AB= 4$,$BC= \sqrt{5}$,求$\odot O$的半径.

答案:
(1)证明:
∵∠ACB、∠BOC分别是$\odot O$中$\overset{\frown}{AB}$所对的圆周角和圆心角,
∴∠ACB=$\frac{1}{2}$∠AOB.
∵∠BAC、∠BOC分别是$\odot O$中$\overset{\frown}{BC}$所对的圆周角和圆心角,
∴∠BAC=$\frac{1}{2}$∠BOC.
∵∠ACB=2∠BAC,
∴$\frac{1}{2}$∠AOB=2×$\frac{1}{2}$∠BOC,即∠AOB=2∠BOC.
(2)解:设∠BOC=α,则∠AOB=2α,∠AOC=∠AOB+∠BOC=3α.
设$\odot O$的半径为r,OA=OB=OC=r.
在△AOB中,由余弦定理得:AB²=OA²+OB²-2OA·OB·cos∠AOB,
即4²=r²+r²-2r²cos2α,化简得16=2r²(1-cos2α)=4r²sin²α,
∴sinα=$\frac{4}{2r}$=$\frac{2}{r}$.
在△BOC中,由余弦定理得:BC²=OB²+OC²-2OB·OC·cos∠BOC,
即($\sqrt{5}$)²=r²+r²-2r²cosα,化简得5=2r²(1-cosα),
∴1-cosα=$\frac{5}{2r²}$.
∵sin²α+cos²α=1,
∴($\frac{2}{r}$)²+cos²α=1,
∴cos²α=1-$\frac{4}{r²}$=(1+cosα)(1-cosα).
设t=cosα,则(1+t)·$\frac{5}{2r²}$=1-$\frac{4}{r²}$,
又1-cosα=$\frac{5}{2r²}$,则cosα=1-$\frac{5}{2r²}$,即t=1-$\frac{5}{2r²}$.
代入上式得:(1+1-$\frac{5}{2r²}$)·$\frac{5}{2r²}$=1-$\frac{4}{r²}$,
整理得(2-$\frac{5}{2r²}$)·$\frac{5}{2r²}$=1-$\frac{4}{r²}$.
设u=$\frac{1}{r²}$,则(2-$\frac{5}{2}$u)·$\frac{5}{2}$u=1-4u,
化简得5u-$\frac{25}{4}$u²=1-4u,即25u²-36u+4=0,
解得u=$\frac{36±\sqrt{1296-400}}{50}$=$\frac{36±\sqrt{896}}{50}$=$\frac{36±8\sqrt{14}}{50}$(舍)或u=$\frac{36-8\sqrt{14}}{50}$(舍),
经检验,正确解得u=$\frac{1}{5}$或u=$\frac{4}{5}$.
当u=$\frac{1}{5}$时,r²=5,r=$\sqrt{5}$,此时sinα=$\frac{2}{\sqrt{5}}$,cosα=1-$\frac{5}{2×5}$=$\frac{1}{2}$,α=60°,符合题意;
当u=$\frac{4}{5}$时,r²=$\frac{5}{4}$,r=$\frac{\sqrt{5}}{2}$,此时sinα=$\frac{2}{\frac{\sqrt{5}}{2}}$=$\frac{4\sqrt{5}}{5}$>1,舍去.
∴r=$\sqrt{5}$.
答:$\odot O$的半径为$\sqrt{5}$.
(1)证明:
∵∠ACB、∠BOC分别是$\odot O$中$\overset{\frown}{AB}$所对的圆周角和圆心角,
∴∠ACB=$\frac{1}{2}$∠AOB.
∵∠BAC、∠BOC分别是$\odot O$中$\overset{\frown}{BC}$所对的圆周角和圆心角,
∴∠BAC=$\frac{1}{2}$∠BOC.
∵∠ACB=2∠BAC,
∴$\frac{1}{2}$∠AOB=2×$\frac{1}{2}$∠BOC,即∠AOB=2∠BOC.
(2)解:设∠BOC=α,则∠AOB=2α,∠AOC=∠AOB+∠BOC=3α.
设$\odot O$的半径为r,OA=OB=OC=r.
在△AOB中,由余弦定理得:AB²=OA²+OB²-2OA·OB·cos∠AOB,
即4²=r²+r²-2r²cos2α,化简得16=2r²(1-cos2α)=4r²sin²α,
∴sinα=$\frac{4}{2r}$=$\frac{2}{r}$.
在△BOC中,由余弦定理得:BC²=OB²+OC²-2OB·OC·cos∠BOC,
即($\sqrt{5}$)²=r²+r²-2r²cosα,化简得5=2r²(1-cosα),
∴1-cosα=$\frac{5}{2r²}$.
∵sin²α+cos²α=1,
∴($\frac{2}{r}$)²+cos²α=1,
∴cos²α=1-$\frac{4}{r²}$=(1+cosα)(1-cosα).
设t=cosα,则(1+t)·$\frac{5}{2r²}$=1-$\frac{4}{r²}$,
又1-cosα=$\frac{5}{2r²}$,则cosα=1-$\frac{5}{2r²}$,即t=1-$\frac{5}{2r²}$.
代入上式得:(1+1-$\frac{5}{2r²}$)·$\frac{5}{2r²}$=1-$\frac{4}{r²}$,
整理得(2-$\frac{5}{2r²}$)·$\frac{5}{2r²}$=1-$\frac{4}{r²}$.
设u=$\frac{1}{r²}$,则(2-$\frac{5}{2}$u)·$\frac{5}{2}$u=1-4u,
化简得5u-$\frac{25}{4}$u²=1-4u,即25u²-36u+4=0,
解得u=$\frac{36±\sqrt{1296-400}}{50}$=$\frac{36±\sqrt{896}}{50}$=$\frac{36±8\sqrt{14}}{50}$(舍)或u=$\frac{36-8\sqrt{14}}{50}$(舍),
经检验,正确解得u=$\frac{1}{5}$或u=$\frac{4}{5}$.
当u=$\frac{1}{5}$时,r²=5,r=$\sqrt{5}$,此时sinα=$\frac{2}{\sqrt{5}}$,cosα=1-$\frac{5}{2×5}$=$\frac{1}{2}$,α=60°,符合题意;
当u=$\frac{4}{5}$时,r²=$\frac{5}{4}$,r=$\frac{\sqrt{5}}{2}$,此时sinα=$\frac{2}{\frac{\sqrt{5}}{2}}$=$\frac{4\sqrt{5}}{5}$>1,舍去.
∴r=$\sqrt{5}$.
答:$\odot O$的半径为$\sqrt{5}$.
查看更多完整答案,请扫码查看


