9. “石头、剪刀、布”是民间广为流传的一种游戏,游戏时甲、乙双方每次做“石头”“剪刀”“布”三种手势中的一种,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛. 假定甲、乙两人每次都是等可能地做这三种手势,那么一次游戏中乙获胜的概率是
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
10. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”,小文购买了“二十四节气”主题邮票,他将“立春”“立夏”“秋分”“大暑”四张邮票背面朝上洗匀放在桌面上(邮票背面完全相同).
(1)小文从中随机抽取一张邮票是“秋分”的概率是______.
(2)小文从中随机抽取一张(不放回),再从中随机抽取一张,请用画树状图或列表的方法求小文抽到的两张邮票恰好是“立春”和“立夏”的概率(这四张邮票依次用字母A,B,C,D表示).
(1)小文从中随机抽取一张邮票是“秋分”的概率是______.
(2)小文从中随机抽取一张(不放回),再从中随机抽取一张,请用画树状图或列表的方法求小文抽到的两张邮票恰好是“立春”和“立夏”的概率(这四张邮票依次用字母A,B,C,D表示).
答案:
(1)$\frac{1}{4}$
(2)解:由题意画树状图如图.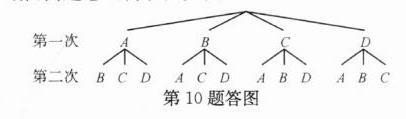
由图可知,共有12种等可能的情况,其中抽到A和B (“立春”和“立夏”)的情况有2种,故小文抽到的两张邮票恰好是“立春”和“立夏”的概率为$\frac{2}{12}=\frac{1}{6}$.
(1)$\frac{1}{4}$
(2)解:由题意画树状图如图.

由图可知,共有12种等可能的情况,其中抽到A和B (“立春”和“立夏”)的情况有2种,故小文抽到的两张邮票恰好是“立春”和“立夏”的概率为$\frac{2}{12}=\frac{1}{6}$.
11. 已知双曲线$y= \frac{k}{x}与直线y= x+2相交于A(-3,m)$,B两点.
(1)直接写出此双曲线的表达式.
(2)若点$M(a,b)$,且a,b都是不大于3的正整数,用画树状图法或列表法求点M在双曲线$y= \frac{k}{x}$上的概率.
(1)直接写出此双曲线的表达式.
(2)若点$M(a,b)$,且a,b都是不大于3的正整数,用画树状图法或列表法求点M在双曲线$y= \frac{k}{x}$上的概率.
答案:
(1)$y=\frac{3}{x}$ 解析:
∵直线$y=x+2$经过点A(-3,m),
∴$m=-3+2=-1$,
∴A(-3,-1),
∴$k=xy=(-3)×(-1)=3$,
∴此双曲线的表达式为$y=\frac{3}{x}$.
(2)列表如下: $(a,b)$123 $1$(1,1)(1,2)(1,3) $2$(2,1)(2,2)(2,3) $3$(3,1)(3,2)(3,3) 由上表可知,一共有9种等可能结果,其中在双曲线上的有2种,则点M 在双曲线上的概率为$\frac{2}{9}$.
(1)$y=\frac{3}{x}$ 解析:
∵直线$y=x+2$经过点A(-3,m),
∴$m=-3+2=-1$,
∴A(-3,-1),
∴$k=xy=(-3)×(-1)=3$,
∴此双曲线的表达式为$y=\frac{3}{x}$.
(2)列表如下: $(a,b)$123 $1$(1,1)(1,2)(1,3) $2$(2,1)(2,2)(2,3) $3$(3,1)(3,2)(3,3) 由上表可知,一共有9种等可能结果,其中在双曲线上的有2种,则点M 在双曲线上的概率为$\frac{2}{9}$.
12. 嘉嘉和淇淇做化学实验,紫色石蕊试剂是一种常用的酸碱指示剂,通常情况下石蕊试剂遇酸溶液变红,遇碱溶液变蓝,遇中性溶液不变色. 现有4瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液,其中白醋溶液、柠檬水溶液是酸性,食用碱溶液是碱性,蒸馏水是中性. 两人各取了4个烧杯,分别倒入这4种不同的无色液体.
(1)嘉嘉将石蕊试剂滴入任意一个烧杯,呈现蓝色的概率是______.
(2)淇淇随机取了两个烧杯,滴入石蕊试剂,用画树状图法或列表法求一杯变红、一杯变蓝的概率.
(1)嘉嘉将石蕊试剂滴入任意一个烧杯,呈现蓝色的概率是______.
(2)淇淇随机取了两个烧杯,滴入石蕊试剂,用画树状图法或列表法求一杯变红、一杯变蓝的概率.
答案:
(1)$\frac{1}{4}$
(2)解:将蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液分别记作A,B,C,D,列表如下: 由表知共有12种可能结果其中一杯变红、一杯变蓝的有4种结果所以一杯变红、一杯变蓝概率为$\frac{4}{12}=\frac{1}{3}$.
由表知共有12种可能结果其中一杯变红、一杯变蓝的有4种结果所以一杯变红、一杯变蓝概率为$\frac{4}{12}=\frac{1}{3}$.
(1)$\frac{1}{4}$
(2)解:将蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液分别记作A,B,C,D,列表如下:
 由表知共有12种可能结果其中一杯变红、一杯变蓝的有4种结果所以一杯变红、一杯变蓝概率为$\frac{4}{12}=\frac{1}{3}$.
由表知共有12种可能结果其中一杯变红、一杯变蓝的有4种结果所以一杯变红、一杯变蓝概率为$\frac{4}{12}=\frac{1}{3}$. 查看更多完整答案,请扫码查看


