《2025年名师金典九年级数学全一册浙教版》

1. 若两个相似三角形的相似比是16:9,则这两个三角形对应边上的高之比是 (A)
A.16:9
B.9:16
C.3:4
D.4:3

答案： A

2. 已知△ABC与△DEF相似,且∠A= ∠D,那么下列结论中,一定成立的是 (D)
A.∠B= ∠E
B.$\frac{AB}{DE}= \frac{AC}{DF}$
C.相似比为$\frac{AB}{DE}$
D.相似比为$\frac{BC}{EF}$

答案： D

3. 如图,点P是等边三角形ABC的重心,AB= 3,Q是BC边上一点,当PQ⊥BP时,则BQ的长为 (D)

A.1
B.$\frac{3}{2}$
C.$\sqrt{3}$
D.2

答案： D

4. 已知两个相似三角形对应边上的高线之比为3:11,那么这两个三角形的相似比为3:11.

答案： 3:11

5. 如图,在△ABC中,D,E分别为AB,AC的中点,连结DE,线段BE,CD相交于点O.若OD= 2,则OC= ______.

4

答案： 4

6. 三角形三边长为5,5,6,则这个三角形的外心$O_1和重心O_2$的距离为$\frac{11}{24}$.

答案： $\frac{11}{24}$

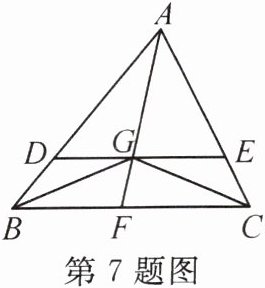
7. 如图,过△ABC的重心G作BC的平行线分别交AB,AC于点D,E,求$\frac{S_{\triangle GBC}}{S_{\triangle ADE}}$的值.

答案：
解:如图，过点A作AM⊥BC于点M,交DE于点N,过点G作GH⊥BC于点H,则GH//AM.
∵DE//BC,G是△ABC的重心，
∴△ADE∽△ABC,AG:AF=DE:BC=2:3,MN=GH,
∴$\frac{AG}{GF}$=$\frac{AN}{MN}$=$\frac{AN}{GH}$=2,
∴$\frac{S_{\triangle GBC}}{S_{\triangle ADE}}$=$\frac{\frac{1}{2}GH \cdot BC}{\frac{1}{2}AN \cdot DE}$=$\frac{GH}{AN}$.$\frac{BC}{DE}$=$\frac{3}{4}$.

8. 如图,在△ABC中,D,E分别是边BC,AB的中点,AD,CE交于点G,求证:$\frac{GE}{CE}= \frac{GD}{AD}= \frac{1}{3}$.

答案：
证明:如图，连结DE.
∵D,E分别是边BC,AB的中点，
∴DE//AC且$\frac{DE}{AC}$=$\frac{1}{2}$,
∴∠DEG=∠ACG,∠GDE=∠GAC,
∴△DEG∽△ACG,
∴$\frac{GE}{GC}$=$\frac{GD}{GA}$=$\frac{DE}{AC}$=$\frac{1}{2}$,
∴$\frac{GE}{GE+CG}$=$\frac{GD}{GD+AG}$=$\frac{1}{3}$
∴$\frac{GE}{CE}$=$\frac{GD}{AD}$=$\frac{1}{3}$.

9. 如图,△ABC的中线AD,BE相交于点F,过点E作EG//AD交BC于点G,则EG:AF的值是 (C)

A.$\frac{1}{2}$
B.$\frac{2}{3}$
C.$\frac{3}{4}$
D.$\frac{4}{5}$

答案： C

10. 如图,在△ABC中,BC= 6,BD是中线,E是BD上一点,作射线AE,交BC于点F.若BE= 2DE,则FC= (C)
A.2
B.2.5
C.3
D.3.5

答案： C

11. 如图,在△ABC中,∠ACB= 90°,AC= 5cm,BC= 7cm,点I为三角形的重心,HI⊥BC于点H,则HI= $\frac{5}{3}$cm.

答案： $\frac{5}{3}$

12. 如图,在△ABC中,D是边AC上的任意一点,点M,N分别是△ABD和△BCD的重心.如果AC= 6,那么线段MN的长为2.

答案： 2