《2025年实验班提优训练八年级数学上册苏科版苏州专版》

1. 手拉手模型 教材 P50 习题 T6·变式 如图,△ABC 和△DEC 都是等边三角形,D 是 BC 延长线上一点,AD 与 BE 相交于点 P,AC,BE 相交于点 M,AD,CE 相交于点 N,则下列五个结论:①AD= BE;②∠BMC= ∠ANC;③∠APM= 60°;④AN= BM;⑤△CMN 是等边三角形.其中,正确的有(D).

A.2 个
B.3 个
C.4 个
D.5 个

答案： D　[解析]
∵△ABC和△DEC都是等边三角形，
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∠ACE=60°,
∴△BCE≌△ACD(SAS),
∴AD=BE.故结论①正确;
∵△BCE≌△ACD,
∴∠CBE=∠CAD.
∵∠ACB=∠ACE=60°,
∴∠BMC=∠ANC.故结论②正确;
∵∠APM是△PBD的外角,
∴∠APM=∠CBE+∠ADC=∠CAD+∠ADC=∠ACB=60°.故结论③正确;
　在△ACN和△BCM中，{∠CAN=∠CBM，AC=BC，∠ACN=∠BCM=60°}，
∴△ACN≌△BCM(ASA),
∴AN=BM.故结论④正确;
∵△ACN≌△BCM,
∴CM=CN.
∵∠MCN=60°,
∴△CMN是等边三角形，
　故结论⑤正确.故选D.

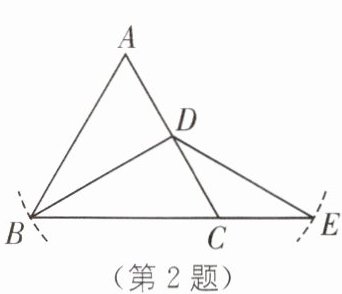
2. (2025·常州金坛期中)如图,BD 是等边三角形 ABC 的边 AC 上的高,以点 D 为圆心,DB 长为半径作弧交 BC 的延长线于点 E,则∠DEC= (C).

A.20°
B.25°
C.30°
D.35°

答案： C　[解析]在等边三角形ABC中,∠ABC=60°,
∵BD是AC边上的高，
∴BD平分∠ABC,
∴∠CBD=$\frac{1}{2}$∠ABC=30°.
∵BD=ED,
∴∠DEC=∠CBD=30°.故选C.

3. 教材 P46 例 3·变式 (2024·无锡锡山区期中)如图,在等边三角形 ABC 中,点 D,E 分别在边 BC,AC 上,且 DE//AB,过点 E 作 EF⊥DE,交 BC 的延长线于点 F.

(1)求∠F 的度数;
(2)若 CD= 2,求 DF 的长.

答案：
(1)
∵△ABC是等边三角形，
∴∠A=∠B=∠ACB=60°.
∵DE//AB,
∴∠B=∠EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°.
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=90°−60°=30°.
(2)
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
∵∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2,
∴CF=2,
∴DF=DC+CF=2+2=4.

4. 等边三角形两条中线相交所成的锐角的度数为( ).

A.30°
B.45°
C.60°
D.75°

答案：
C　[解析]如图,△ABC为等边三角形，BD,CE分别为边AC，AB上的中线，交于点O，
∴CE⊥AB,BD平分∠ABC,
∴∠OEB=90°,∠EBO=$\frac{1}{2}$∠ABC =30°,
∴∠BOE=90°−30°=60°.故选C.
　思路引导　本题主要考查等边三角形的性质，掌握等边三角形每边上的中线、高和对角的平分线相互重合是解题的关键.
　

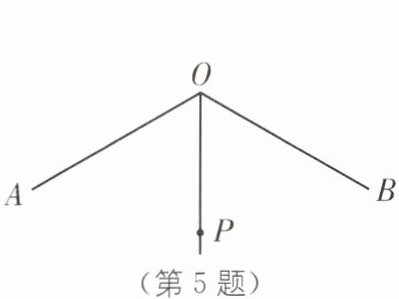
5. (2024·宿迁宿城区期末)如图,∠AOB= 120°,OP 平分∠AOB,且 OP= 1.若点 M,N 分别在 OA,OB 上,且△PMN 为等边三角形,则满足上述条件的△PMN 有( ).

A.1 个
B.2 个
C.3 个
D.无数个

答案：
D　[解析]如图,过点P作PM⊥OA于M,PN⊥OB 于N.
∵OP平分∠AOB,PM⊥OA于M,PN⊥OB于N,
∴PM=PN,∠PMO=90°,∠PNO=90°.
∴∠MPN=360°−∠AOB−∠PMO−∠PNO=60°,
∴此时,△PMN是等边三角形.
　当M向MO方向移动,N向NB方向移动,∠MPM₁=∠NPN₁时，
　∠M₁PN₁=∠M₁PN+∠NPN₁=∠M₁PN+∠MPM₁=∠MPN=60°，
　在△PMM₁和△PNN₁中，{∠PMM₁=∠PNN₁，PM=PN，∠MPM₁=∠NPN₁}，
∴△PMM₁≌△PNN₁(ASA),
∴PM₁=PN₁,
∴△M₁PN₁是等边三角形.
∴当M向MO方向移动,N向NB方向移动，∠MPM₁=∠NPN₁时,△M₁PN₁是等边三角形.
　同理:当M向MA方向移动,N向NO方向移动，也存在无数个满足条件的等边三角形PMN.
　综上所述,满足条件的△PMN有无数个.故选D.
　

6. 如图,等边三角形纸片 ABC 的边长为 6,E,F 是边 BC 上的三等分点.分别过点 E,F 沿着平行于 BA,CA 方向各剪一刀,则剪下的△DEF 的周长是6.

答案： 6

7. 以正方形 ABCD 的一边 CD 为边作等边三角形 CDE.连接 AE,BE.
(1)画出图形;
(2)求∠AEB 的度数.

答案：

(1)当点E在正方形ABCD外时，如图
(1);
　当点E在正方形ABCD内时，如图
(2).

(2)在图
(1)中，
∵∠ADE=∠ADC+∠CDE=90°+60°=150°,AD=CD=DE,
∴∠DEA=∠DAE=15°.同理∠CEB=15°.
∴∠AEB=∠DEC−∠DEA−∠CEB=60°−15°−15°=30°.
　在图
(2)中,
∵AD=CD=DE,∠ADE=∠ADC−∠CDE=90°−60°=30°,
∴∠AED=∠DAE=75°.同理∠CEB=75°.
∴∠AEB=360°−∠AED−∠CEB−∠CED=360°−75°−75°−60°=150°.
　综上所述，∠AEB的度数为30°或150°.
　

8. (2025·扬州广陵区期中)已知:如图,在四边形 ABCD 中,∠ABC= ∠ADC= 90°,点 E 是 AC 的中点.
(1)求证:△BED 是等腰三角形;
∵∠ABC=∠ADC=90°,点E是AC边的中点，∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,∴BE=DE,∴△BED是等腰三角形.
(2)当∠BCD= 150°时,△BED 是等边三角形.

答案：
(1)
∵∠ABC=∠ADC=90°,点E是AC边的中点，
∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,
∴BE=DE,
∴△BED是等腰三角形.
(2)150　[解析]
∵AE=ED,
∴∠DAE=∠EDA.
∵AE=BE,
∴∠EAB=∠EBA.
∵∠DAE+∠EDA=∠DEC,
　∠EAB+∠EBA=∠BEC,
∴∠DAB=$\frac{1}{2}$∠DEB.
∵△BED是等边三角形,
∴∠DEB=60°,
∴∠BAD=30°,
∴∠BCD=360°−90°−90°−30°=150°.
　归纳总结　此题主要考查了等腰三角形的性质和判定以及三角形外角的性质等知识，根据题意得出$\frac{1}{2}$∠DEB=∠DAB是解题关键.