《2025年实验班提优训练八年级数学上册苏科版苏州专版》

1. (教材 P6 练习 T1·变式)(2025·苏州姑苏区期中)下列每组数表示三根木棒的长度,将它们首尾相接后,能摆成三角形的是(D).
A.2,3,5
B.3,4,8
C.7,4,2
D.3,3,4

答案： D [解析] A.2+3=5,无法构成三角形;
B.3+4＜8,无法构成三角形;
C.2+4＜7,无法构成三角形;
D.3+3＞4,4-3＜3,可以构成三角形.
故选D.

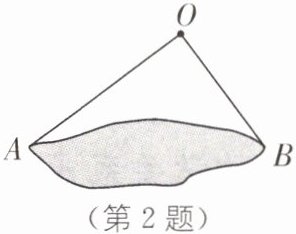
2. (2025·南通启东期中)如图,为估计池塘两岸 A,B 间的距离,小明在池塘一侧选取了一点 O,测得 OA= 16 m,OB= 12 m,那么 AB 的距离不可能是(D).

A.5 m
B.15 m
C.20 m
D.30 m
]

答案： D [解析] 根据三角形的三边关系可得16-12＜AB＜16+12,即4＜AB＜28,
∴30 m不可能.故选D.

3. (2024·淮安中考)用一根小木棒与两根长度分别为 3 cm,5 cm 的小木棒组成三角形,则这根小木棒的长度可以是(B).
A.9 cm
B.7 cm
C.2 cm
D.1 cm

答案： B [解析] 设第三根木棒长为x cm,由三角形三边关系定理得5-3＜x＜5+3,
所以x的取值范围是2＜x＜8,
观察选项,只有选项B符合题意.故选B.
归纳总结 设三角形的两边长为a,b(a＞b),则第三边长x的取值范围为a-b＜x＜a+b.

4. (2024·苏州姑苏区二模)若某三角形的三边长分别为 3,4,m,则 m 的值可以是(B).
A.1
B.5
C.7
D.9

答案： B [解析] 根据三角形的三边关系定理,
得4-3＜m＜4+3,
解得1＜m＜7,即符合条件的选项只有B.
故选B.

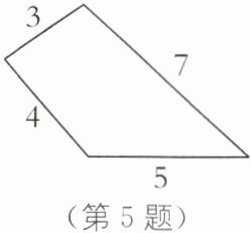
5. (2024·扬州广陵区期末)如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为 3,4,5,7,且相邻两木条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任两螺丝的距离的最大值是(C).

A.7
B.8
C.9
D.10

答案： C [解析] 已知4条木条的长分别为3,4,5,7.
①选3+4,5,7作为三角形,则三边长为7,5,7.7-5＜7＜7+5,能构成三角形,此时两个螺丝间的最长距离为7;
②选4+5,3,7作为三角形,则三边长为9,3,7.7-3＜9＜7+3,能构成三角形,此时两个螺丝间的最大距离为9;
③选3+7,4,5作为三角形,则三边长为10,4,5.4+5＜10,不能构成三角形,此种情况不成立;
④选5+7,3,4作为三角形,则三边长为12,3,4.而3+4＜12,不能构成三角形,此种情况不成立.
综上所述,任两螺丝的距离的最大值为9.
故选C.

6. 把一条长 15 厘米的线段截成三段,使每条线段的长度都是整数,用三条线段可以组成7个不同的三角形.

答案： 7 [解析] 根据三角形三边关系,三条线段可以组成三角形的有:①1,7,7;②2,6,7;③3,5,7;④3,6,6;⑤4,5,6;⑥5,5,5;⑦4,4,7.故可以组成7个不同的三角形.

7. (教材 P6 练习 T3·变式)在△ABC 中,若∠C 为钝角,则在该三角形中的最大边是AB.

答案： AB

8. 如图,已知 P 是△ABC 内一点,试说明 PA+PB+PC＞$\frac{1}{2}$(AB+BC+AC).
]

答案： 已知在△ABP中,AP+BP＞AB.
同理可得BP+PC＞BC,AP+PC＞AC.
以上三式分别相加,得
2(PA+PB+PC)＞AB+BC+AC,
即PA+PB+PC＞$\frac{1}{2}$(AB+BC+AC).

9. (2025·河北唐山路南区期中)使用 a,b 两根直的铁丝做成一个三角形框架,尺寸如图所示,若需要将其中一根铁丝折成两段,则可以把铁丝分为两段的是(B).
A.只有 a
B.只有 b
C.a,b 都可以
D.a,b 都不可以

答案： B [解析]
∵a＜b,
∴由三角形三边关系定理得到:只有将铁丝b折成两段才能做成一个三角形框架.故选B.

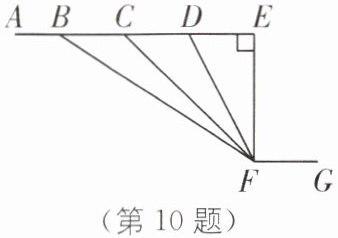
10. (2024·安徽合肥庐阳区期末)如图,从点 A 到点 G,下列路径最短的是(A).

A.A→B→F→G
B.A→C→F→G
C.A→D→F→G
D.A→E→F→G

答案： A [解析] 根据三角形两边之和大于第三边可知A→B→F→G路径最短.故选A.

11. 如图是一个直三棱柱的表面展开图,其中 AD= 10,CD= 2,则下列可作为 AB 长度的是(B).
A.5
B.4
C.3
D.2

答案： B [解析] 由题图可知,AD=AB+BC+CD.
∵AD=10,CD=2,
∴AB+BC=8.
设AB=x,则BC=8-x.
由三角形三边关系,得$\left\{\begin{array}{l} 8-x＜x+2,\\ 8-x＞x-2,\end{array}\right. $
解得3＜x＜5,
∴AB的长度可以是4.故选B.
方法诠释 解答本题时需要根据题图得出AD=AB+BC+CD,再根据AD=10,CD=2,得出AB+BC=8,然后设AB=x,得出BC=8-x,最后根据三角形的三边关系列出不等式组,求得AB的取值范围,然后求出问题的答案.