2025年实验班提优训练八年级数学上册苏科版苏州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练八年级数学上册苏科版苏州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. (湖南衡阳自主招生)甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度 y(m)与挖掘时间 x(h)之间的关系如图所示,根据图象所提供的信息,其中不正确的是(
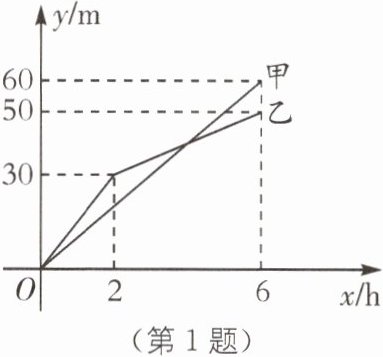
A.甲队挖掘 30 m 时,用了 3 h
B.挖掘 5 h 时甲队比乙队多挖了 5 m
C.乙队的挖掘速度总是小于甲队
D.开挖后甲、乙两队所挖河渠长度相等时,x= 4
C
).
A.甲队挖掘 30 m 时,用了 3 h
B.挖掘 5 h 时甲队比乙队多挖了 5 m
C.乙队的挖掘速度总是小于甲队
D.开挖后甲、乙两队所挖河渠长度相等时,x= 4
答案:
C [解析]由图象,可得甲队的速度为60÷6 = 10(m/h). 故甲队挖掘30m,用时30÷10 = 3(h). 故A正确;当x>2时,乙队的速度为(50 - 30)÷(6 - 2) = 5(m/h),故挖掘5h时甲队比乙队多挖了10×5 - [30+(5 - 2)×5] = 5(m). 故B正确;前2h乙队挖得快,在2~6h之间,甲队挖得快. 故C错误;当2<x<6时,令[30 + 5(x - 2)] - 10x = 0,得x = 4. 故D正确. 故选C.
2. (2025·泰州姜堰区期末)如图,购买一种苹果所付款金额 y(元)与购买量 x(千克)之间的函数图象由线段 OA 和射线 AB 组成,若一次购买 5 千克这种苹果所付金额为$ y_1($元),购买五次 1 千克所付金额为$ y_2($元),则$ y_2-y_1= $
6
.
答案:
6 [解析]由图象可得,2千克以内,每千克苹果的单价为20÷2 = 10(元),当x≥2时,设y与x的函数表达式为y = kx + b.
∵点(2,20),(4,36)在该函数图象上,
∴{2k + b = 20,4k + b = 36,解得{k = 8,b = 4,即当x≥2时,y与x的函数表达式为y = 8x + 4,y1 = 8×5 + 4 = 44,y2 = 10×5 = 50,
∴y2 - y1 = 50 - 44 = 6.
∵点(2,20),(4,36)在该函数图象上,
∴{2k + b = 20,4k + b = 36,解得{k = 8,b = 4,即当x≥2时,y与x的函数表达式为y = 8x + 4,y1 = 8×5 + 4 = 44,y2 = 10×5 = 50,
∴y2 - y1 = 50 - 44 = 6.
3. 为增加校园绿化面积,某校计划购买甲、乙两种树苗.已知购买 20 棵甲种树苗和 16 棵乙种树苗共花费 1280 元,购买 1 棵甲种树苗比 1 棵乙种树苗多花费 10 元.
(1)求甲、乙两种树苗每棵的价格分别是多少元.
(2)若购买甲、乙两种树苗共 100 棵,且购买乙种树苗的数量不超过甲种树苗的 3 倍.则购买甲、乙两种树苗各多少棵时花费最少?请说明理由.
(1)求甲、乙两种树苗每棵的价格分别是多少元.
(2)若购买甲、乙两种树苗共 100 棵,且购买乙种树苗的数量不超过甲种树苗的 3 倍.则购买甲、乙两种树苗各多少棵时花费最少?请说明理由.
答案:
(1)设甲种树苗每棵的价格是x元,乙种树苗每棵的价格是y元. 由题意,得{20x + 16y = 1280,x - y = 10,解得{x = 40,y = 30.故甲种树苗每棵的价格是40元,乙种树苗每棵的价格是30元.
(2)购买甲种树苗25棵,乙种树苗75棵,花费最少. 理由如下:设购买两种树苗共花费W元,购买甲种树苗m棵,则购买乙种树苗(100 - m)棵.
∵购买乙种树苗的数量不超过甲种树苗的3倍,
∴100 - m≤3m,解得m≥25. 根据题意,得W = 40m + 30(100 - m) = 10m + 3000.
∵10>0,
∴W随m的增大而增大,
∴当m = 25时,W取最小值,最小值为10×25 + 3000 = 3250(元),此时100 - m = 75. 故购买甲种树苗25棵,乙种树苗75棵,花费最少.
(1)设甲种树苗每棵的价格是x元,乙种树苗每棵的价格是y元. 由题意,得{20x + 16y = 1280,x - y = 10,解得{x = 40,y = 30.故甲种树苗每棵的价格是40元,乙种树苗每棵的价格是30元.
(2)购买甲种树苗25棵,乙种树苗75棵,花费最少. 理由如下:设购买两种树苗共花费W元,购买甲种树苗m棵,则购买乙种树苗(100 - m)棵.
∵购买乙种树苗的数量不超过甲种树苗的3倍,
∴100 - m≤3m,解得m≥25. 根据题意,得W = 40m + 30(100 - m) = 10m + 3000.
∵10>0,
∴W随m的增大而增大,
∴当m = 25时,W取最小值,最小值为10×25 + 3000 = 3250(元),此时100 - m = 75. 故购买甲种树苗25棵,乙种树苗75棵,花费最少.
4. (湖北襄阳自主招生)某部影片的盈利额(即影片的票房收入与固定成本之差)记为 y,观影人数记为 x,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后 y 与 x 的函数图象.给出下列四种说法:
①图(2)对应的方案是提高票价,并提高成本;
②图(2)对应的方案是保持票价不变,并降低成本;
③图(3)对应的方案是提高票价,并保持成本不变;
④图(3)对应的方案是提高票价,并降低成本.
其中,正确的说法是(

A.①③
B.①④
C.②③
D.②④
①图(2)对应的方案是提高票价,并提高成本;
②图(2)对应的方案是保持票价不变,并降低成本;
③图(3)对应的方案是提高票价,并保持成本不变;
④图(3)对应的方案是提高票价,并降低成本.
其中,正确的说法是(
C
).
A.①③
B.①④
C.②③
D.②④
答案:
C [解析]由题图
(1)可知,点A的纵坐标的相反数表示成本,直线的倾斜程度越大表示票价越高. 题图
(2)对应的方案是保持票价不变,并降低成本. 故①错误,②正确;题图
(3)对应的方案是提高票价,并保持成本不变. 故③正确,④错误. 故选C.
(1)可知,点A的纵坐标的相反数表示成本,直线的倾斜程度越大表示票价越高. 题图
(2)对应的方案是保持票价不变,并降低成本. 故①错误,②正确;题图
(3)对应的方案是提高票价,并保持成本不变. 故③正确,④错误. 故选C.
5. (2025·无锡期末)如图,甲、乙两车从 A 城出发匀速行驶到 B 城.在整个行驶过程中,甲、乙两车距离 B 城的距离 y(km)与甲车行驶的时间 t(h)之间的函数关系如图所示,则甲、乙两车相距 50 千米时,t 的值为
$\frac{25}{36}$或$\frac{35}{24}$或$\frac{85}{24}$或$\frac{155}{36}$
.
答案:
$\frac{25}{36}$或$\frac{35}{24}$或$\frac{85}{24}$或$\frac{155}{36}$ [解析]设甲车距离B城的距离y1与甲车行驶的时间t之间的函数关系为y1 = k1t + b1(k1,b1为常数,且k1≠0). 将坐标(0,360)和(5,0)分别代入y1 = k1t + b1,得{b1 = 360,5k1 + b1 = 0,解得{k1 = - 72,b1 = 360,
∴甲车距离B城的距离y1与甲车行驶的时间t之间的函数关系为y1 = - 72t + 360(0≤t≤5);当1<t≤4时,设乙车距离B城的距离y2与甲车行驶的时间t之间的函数关系为y2 = k2t + b2(k2,b2为常数,且k2≠0). 将坐标(1,360)和(4,0)分别代入y2 = k2t + b2,得{k2 + b2 = 360,4k2 + b2 = 0,解得{k2 = - 120,b2 = 480,
∴当1<t≤4时,乙车距离B城的距离y2与甲车行驶的时间t之间的函数关系为y2 = - 120t + 480,
∴乙车距离B城的距离y2与甲车行驶的时间t之间的函数关系为y2 = {360(0≤t≤1),- 120t + 480(1<t≤4),0(4<t≤5).当0≤t≤1时,甲、乙两车相距50千米时,得360 - (- 72t + 360) = 50,解得t = $\frac{25}{36}$;当1<t≤4时,甲、乙两车相距50千米时,得|- 72t + 360 - (- 120t + 480)| = 50,解得t = $\frac{35}{24}$或$\frac{85}{24}$;当4<t≤5时,甲、乙两车相距50千米时,得 - 72t + 360 = 50,解得t = $\frac{155}{36}$.
∴t的值为$\frac{25}{36}$或$\frac{35}{24}$或$\frac{85}{24}$或$\frac{155}{36}$.
∴甲车距离B城的距离y1与甲车行驶的时间t之间的函数关系为y1 = - 72t + 360(0≤t≤5);当1<t≤4时,设乙车距离B城的距离y2与甲车行驶的时间t之间的函数关系为y2 = k2t + b2(k2,b2为常数,且k2≠0). 将坐标(1,360)和(4,0)分别代入y2 = k2t + b2,得{k2 + b2 = 360,4k2 + b2 = 0,解得{k2 = - 120,b2 = 480,
∴当1<t≤4时,乙车距离B城的距离y2与甲车行驶的时间t之间的函数关系为y2 = - 120t + 480,
∴乙车距离B城的距离y2与甲车行驶的时间t之间的函数关系为y2 = {360(0≤t≤1),- 120t + 480(1<t≤4),0(4<t≤5).当0≤t≤1时,甲、乙两车相距50千米时,得360 - (- 72t + 360) = 50,解得t = $\frac{25}{36}$;当1<t≤4时,甲、乙两车相距50千米时,得|- 72t + 360 - (- 120t + 480)| = 50,解得t = $\frac{35}{24}$或$\frac{85}{24}$;当4<t≤5时,甲、乙两车相距50千米时,得 - 72t + 360 = 50,解得t = $\frac{155}{36}$.
∴t的值为$\frac{25}{36}$或$\frac{35}{24}$或$\frac{85}{24}$或$\frac{155}{36}$.
查看更多完整答案,请扫码查看


