2025年实验班提优训练八年级数学上册苏科版苏州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练八年级数学上册苏科版苏州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. 下列条件中,不能判定两个直角三角形全等的是(
A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
C
).A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
答案:
C [解析] A. 一个锐角和斜边对应相等,正确,符合判定定理AAS;B. 两条直角边对应相等,正确,符合判定定理SAS;C. 全等三角形的判定必须要有边的参与,不正确;D. 斜边和一条直角边对应相等,正确,符合判定定理HL. 故选C.
2. (2025·盐城盐都区月考)如图,EC⊥BD,垂足为 C,A 是 EC 上一点,且 AC= CD,AB= DE. 若 AC= 3.5,BD= 9,则 AE 的长为(
A.2
B.2.5
C.3
D.5.5
A
).A.2
B.2.5
C.3
D.5.5
答案:
A [解析]
∵EC⊥BD,
∴∠ACB = ∠DCE = 90°. 在Rt△ABC和Rt△DEC中,$\begin{cases} AB = DE, \\ AC = DC, \end{cases}$
∴Rt△ABC≌Rt△DEC(HL).
∴CB = CE,AC = CD = 3.5.
∵BD = CB + CD = 9,
∴CB = 5.5,
∴CE = 5.5,
∴AE = CE - AC = 5.5 - 3.5 = 2. 故选A.
∵EC⊥BD,
∴∠ACB = ∠DCE = 90°. 在Rt△ABC和Rt△DEC中,$\begin{cases} AB = DE, \\ AC = DC, \end{cases}$
∴Rt△ABC≌Rt△DEC(HL).
∴CB = CE,AC = CD = 3.5.
∵BD = CB + CD = 9,
∴CB = 5.5,
∴CE = 5.5,
∴AE = CE - AC = 5.5 - 3.5 = 2. 故选A.
3. (2025·南京玄武区期中)如图,在△ABC 中,AD⊥BC 于点 D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件:

AB = AC
.
答案:
AB = AC [解析] 还需添加条件AB = AC.
∵AD⊥BC于D,
∴∠ADB = ∠ADC = 90°. 在Rt△ABD和Rt△ACD中,$\begin{cases} AB = AC, \\ AD = AD, \end{cases}$
∴Rt△ABD≌Rt△ACD(HL).
∵AD⊥BC于D,
∴∠ADB = ∠ADC = 90°. 在Rt△ABD和Rt△ACD中,$\begin{cases} AB = AC, \\ AD = AD, \end{cases}$
∴Rt△ABD≌Rt△ACD(HL).
4. 教材 P30 习题 T2·变式 (2025·苏州姑苏区期中)如图,在△ABE 与△CBD 中,AE⊥BD 于点 E,CD⊥BD 于点 D,AB= BC,BE= CD. 证明:△ABE≌△BCD.
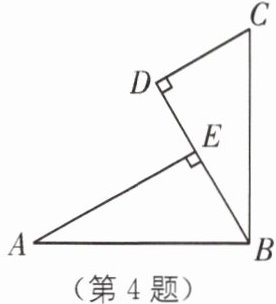

答案:
∵AE⊥BD,CD⊥BD,
∴∠AEB = ∠BDC = 90°. 在Rt△ABE和Rt△BCD中,$\begin{cases} AB = BC, \\ BE = CD, \end{cases}$
∴Rt△ABE≌Rt△BCD(HL).
∵AE⊥BD,CD⊥BD,
∴∠AEB = ∠BDC = 90°. 在Rt△ABE和Rt△BCD中,$\begin{cases} AB = BC, \\ BE = CD, \end{cases}$
∴Rt△ABE≌Rt△BCD(HL).
5. (2024·苏州吴中区期中)如图,PD⊥AB,PE⊥AC,垂足分别为 D,E,且 PD= PE,则△APD 与△APE 全等的直接理由是(

A.SSS
B.AAS
C.HL
D.ASA
C
).
A.SSS
B.AAS
C.HL
D.ASA
答案:
C [解析]
∵PD⊥AB,PE⊥AC,
∴∠ADP = ∠AEP = 90°. 在Rt△APD和Rt△APE中,$\begin{cases} PD = PE, \\ AP = AP, \end{cases}$
∴Rt△APD≌Rt△APE(HL). 故选C.
∵PD⊥AB,PE⊥AC,
∴∠ADP = ∠AEP = 90°. 在Rt△APD和Rt△APE中,$\begin{cases} PD = PE, \\ AP = AP, \end{cases}$
∴Rt△APD≌Rt△APE(HL). 故选C.
6. 教材 P32 习题 T12·变式 (2025·镇江期中)如图,BE= CF,AE⊥BC,DF⊥BC,要根据“HL”证明 Rt△ABE≌Rt△DCF,则还需要添加一个条件是(
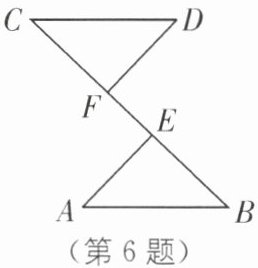
A.AE= DF
B.∠A= ∠D
C.∠B= ∠C
D.AB= DC
D
).
A.AE= DF
B.∠A= ∠D
C.∠B= ∠C
D.AB= DC
答案:
D [解析] 条件是AB = CD. 理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD = ∠AEB = 90°. 在Rt△ABE和Rt△DCF中,$\begin{cases} AB = DC, \\ BE = CF, \end{cases}$
∴Rt△ABE≌Rt△DCF(HL). 故选D.
∵AE⊥BC,DF⊥BC,
∴∠CFD = ∠AEB = 90°. 在Rt△ABE和Rt△DCF中,$\begin{cases} AB = DC, \\ BE = CF, \end{cases}$
∴Rt△ABE≌Rt△DCF(HL). 故选D.
7. (2024·常州二十四中月考)如图,在 Rt△ABC 中,∠C= 90°,AC= 10,BC= 5,线段 PQ= AB,P,Q 两点分别在 AC 和过点 A 且垂直于 AC 的射线 AO 上运动,则当 AP=

5或10
时,△ABC 和△PQA 全等.
答案:
5或10 [解析]
∵∠C = 90°,AO⊥AC,
∴∠C = ∠QAP = 90°. ①当AP = 5 = BC时,在Rt△ACB和Rt△QAP中,$\begin{cases} AB = QP, \\ CB = AP, \end{cases}$
∴Rt△ACB≌Rt△QAP(HL);②当AP = 10 = AC时,在Rt△ACB和Rt△PAQ中,$\begin{cases} AB = PQ, \\ AC = PA, \end{cases}$
∴Rt△ACB≌Rt△PAQ(HL).
∵∠C = 90°,AO⊥AC,
∴∠C = ∠QAP = 90°. ①当AP = 5 = BC时,在Rt△ACB和Rt△QAP中,$\begin{cases} AB = QP, \\ CB = AP, \end{cases}$
∴Rt△ACB≌Rt△QAP(HL);②当AP = 10 = AC时,在Rt△ACB和Rt△PAQ中,$\begin{cases} AB = PQ, \\ AC = PA, \end{cases}$
∴Rt△ACB≌Rt△PAQ(HL).
8. 实验班原创 如图,点 B,F,C,E 在同一直线上,AC 与 DF 相交于点 G,AB⊥BE,垂足为 B,DE⊥BE,垂足为 E,且 AC= DF,BF= CE.
(1)求证:△ABC≌△DEF;
(2)若∠A= 70°,求∠AGF 的度数.

(1)求证:△ABC≌△DEF;
(2)若∠A= 70°,求∠AGF 的度数.

答案:
(1)
∵AB⊥BE,
∴∠B = 90°.
∵DE⊥BE,
∴∠E = 90°.
∵BF = CE,
∴BF + CF = CE + CF,即BC = EF. 在Rt△ABC和Rt△DEF中,$\begin{cases} AC = DF, \\ BC = EF, \end{cases}$
∴Rt△ABC≌Rt△DEF(HL).
(2)
∵∠A = 70°,∠B = 90°,
∴∠ACB = 90° - 70° = 20°. 由
(1)知,Rt△ABC≌Rt△DEF,
∴∠DFE = ∠ACB = 20°,
∴∠AGF = ∠ACB + ∠DFE = 40°.
(1)
∵AB⊥BE,
∴∠B = 90°.
∵DE⊥BE,
∴∠E = 90°.
∵BF = CE,
∴BF + CF = CE + CF,即BC = EF. 在Rt△ABC和Rt△DEF中,$\begin{cases} AC = DF, \\ BC = EF, \end{cases}$
∴Rt△ABC≌Rt△DEF(HL).
(2)
∵∠A = 70°,∠B = 90°,
∴∠ACB = 90° - 70° = 20°. 由
(1)知,Rt△ABC≌Rt△DEF,
∴∠DFE = ∠ACB = 20°,
∴∠AGF = ∠ACB + ∠DFE = 40°.
查看更多完整答案,请扫码查看


