《2025年实验班提优训练八年级数学上册苏科版苏州专版》

9. (2024·上海崇明区期末)如图，AD 为△ABC 的角平分线，DE//AB 交 AC 于点 E，若$\angle BAC=100^{\circ}$，则$\angle ADE=$50°.

答案： 50　[解析]
∵AD为△ABC的角平分线，∠BAC=100°，
∴∠BAD=∠CAD=$\frac{1}{2}×100°=50°$.
∵DE//AB，
∴∠ADE=∠BAD=50°.

10. (2025·北京朝阳区期中)在△ABC 中，AB＞AC，D，E 是 BC 边上的两点，且 BD＜BE，有下列四个推断：
①若 AD 是△ABC 的高，则 AE 可能是△ABC 的中线；
②若 AD 是△ABC 的中线，则 AE 可能是△ABC 的高；
③若 AD 是△ABC 的角平分线，则 AE 可能是△ABC 的中线；
④若 AD 是△ABC 的高，则 AE 不可能是△ABC 的角平分线.
上述推断中所有正确结论的序号是②④.

答案： ②④　[解析]①
∵AB＞AC，AD是△ABC的高，
∴AE不可能是△ABC的中线，此推断错误；
②AD是△ABC的中线，则AE可能是△ABC的高，此推断正确；
③AD是△ABC的角平分线，则AE不可能是△ABC的中线，此推断错误；
④AD是△ABC的高，则AE不可能是△ABC的角平分线，此推断正确.故所有正确结论的序号为②④.

11. 在△ABC 中，D 是 BC 的中点，AB = 12，AC = 8. 用剪刀从点 D 入手进行裁剪，若沿 DA 剪成两个三角形，则它们周长的差为______；若点 E 在 AB 上，沿 DE 剪开得到两部分周长差为 2，则 AE =______.

答案：
4　1或3　[解析]如图
(1)，
∵D是BC的中点，
∴BD=CD，
∴△ABD的周长-△ACD的周长=AB+BD+AD-(AC+CD+AD)=AB-AC=4.
如图
(2)，设AE=x，则BE=12-x，
①当四边形ACDE的周长-△BDE的周长=2时，即AE+ED+CD+AC-(BE+BD+DE)=2，整理，得AE+AC-BE=2，
∴x+8-(12-x)=2，解得x=3；
②当△BDE的周长-四边形ACDE的周长=2时，即BE+BD+DE-(AE+ED+CD+AC)=2，整理，得BE-AE-AC=2，
∴12-x-x-8=2，解得x=1.
综上所述，AE=1或3.

12. (2025·广东珠海香洲区期末)如图，点 A，B，C分别是线段 BD，CE，AF 的中点，若△DEF 的面积为 a，则△ABC 的面积为______.（用含 a 的式子表示）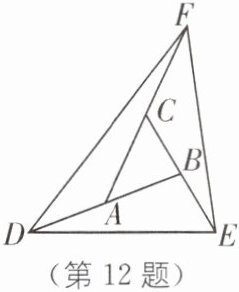

答案：
$\frac{1}{7}a$ [解析]如图，连接AE，CD，令△ABC的面积为x，
∵点B为CE的中点，
∴$S_{\triangle ABE}=S_{\triangle ABC}=x$.同理可得$S_{\triangle ADE}=x$，$S_{\triangle ACD}=S_{\triangle FCD}=x$，$S_{\triangle FCE}=2x$，
∴$S_{\triangle DEF}=7x$.又△DEF的面积为a，
∴7x=a，则x=$\frac{1}{7}a$.
∴△ABC的面积为$\frac{1}{7}a$.

13. 在△ABC 中,$AB:AC =3:2$,$BC=AC +1$,若△ABC 的中线 BD把△ABC 的周长分成两部分的比是$8:7$,求边 AB,AC 的长.

答案： 设AB=3x，则AC=2x，AD=CD=x，BC=2x+1.分两种情况讨论：
①当(AB+AD):(BC+CD)=8:7，即7AB=8BC+CD时，由题意，得7×3x=8(2x+1)+x，解得x=2，则AB=6，AC=4；
②当(BC+CD):(AB+AD)=8:7，即7BC=8AB+AD时，由题意，得7(2x+1)=8×3x+x，解得x=$\frac{7}{11}$，则AB=$\frac{21}{11}$，AC=$\frac{14}{11}$.
综上所述，AB=6，AC=4或AB=$\frac{21}{11}$，AC=$\frac{14}{11}$.

[整体思想] [中考新考法] [满足条件 的结论开放]如图,在△ABC中,$AD\perp BC$,AE平分$\angle BAC$,$\angle B=70^{\circ}$,$\angle C=30^{\circ}$.
(1)求$\angle BAE$的度数.
(2)求$\angle DAE$的度数.
(3)探究:如果条件$\angle B=70^{\circ}$,$\angle C=30^{\circ}$改成$\angle B-\angle C=40^{\circ}$,是否也能得出$\angle DAE$的度数?若能,请你写出求解过程;若不能,请说明理由.

答案：
(1)
∵∠B+∠C+∠BAC=180°，
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°.
∵AE平分∠BAC，
∴∠BAE=$\frac{1}{2}$∠BAC=40°.
(2)
∵AD⊥BC，
∴∠ADB=90°.又∠ADB+∠B+∠BAD=180°，
∴∠BAD=180°-90°-70°=20°，
∴∠DAE=∠BAE-∠BAD=40°-20°=20°.
(3)能.理由如下：
∵∠B+∠C+∠BAC=180°，
∴∠BAC=180°-∠B-∠C.
∵AE平分∠BAC，
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}×(180°-∠B-∠C)=90°-\frac{1}{2}(∠B+∠C)$.
∵AD⊥BC，
∴∠ADB=90°.又∠ADB+∠B+∠BAD=180°，
∴∠BAD=90°-∠B，
∴∠DAE=∠BAE-∠BAD=90°-$\frac{1}{2}(∠B+∠C)$-(90°-∠B)=$\frac{1}{2}(∠B-∠C)$.
∵∠B-∠C=40°，
∴∠DAE=$\frac{1}{2}×40°=20°$.

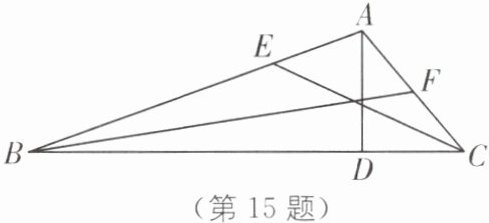
15.(2024·浙江温州期中)如图,$AD$是△ABC的高,$CE$是的△ACB角平分线,$F$是的AC中点,$\angle ACB=50^{\circ}$,$\angle BAD=70^{\circ}$.
(1)求$\angle AEC$度数.
(2)若△BCF与△BAF周长差为3,$AB=7$,能否求出BC的值?若能,请写出理由和结果;若不能,请你补条件并解答.

答案：
(1)
∵AD是△ABC的高，
∴∠ADC=90°.
∵∠ACB=50°，
∴∠CAD=40°.又∠BAD=70°，
∴∠BAC=70°+40°=110°.
∵CE为∠ACB的平分线，
∴∠ACE=$\frac{1}{2}$∠ACB=25°，
∴∠AEC=180°-∠BAC-∠ACE=180°-110°-25°=45°.
(2)能求出BC的值.理由如下：
∵F是AC中点，
∴AF=FC.
∵△BCF与△BAF的周长差为3，
∴(BC+CF+BF)-(AB+AF+BF)=3，
∴BC-AB=3.
∵AB=7，
∴BC=3+7=10.