《2025年综合应用创新题典中点六年级数学上册北师大版》

1. 计算下列各题。
$\frac{2}{5}+\frac{9}{8}×\frac{5}{9}+\frac{3}{8}$
$\frac{11}{18}÷[2-(\frac{1}{4}+\frac{1}{6})]$

答案： $\frac{2}{5}+\frac{9}{8}×\frac{5}{9}+\frac{3}{8}$ $\frac{11}{18}÷\left[2-\left(\frac{1}{4}+\frac{1}{6}\right)\right]$
$=\frac{2}{5}+\frac{5}{8}+\frac{3}{8}$ $=\frac{11}{18}÷\left[2-\frac{5}{12}\right]$
$=\frac{2}{5}+\left(\frac{5}{8}+\frac{3}{8}\right)$ $=\frac{11}{18}÷\frac{19}{12}$
$=\frac{2}{5}+1$ $=\frac{22}{57}$
$=\frac{7}{5}$

2. 用简便方法计算。
$(35×15)×\frac{7}{35}×\frac{2}{15}$
$6×(\frac{5}{6}-\frac{5}{8})×8$

答案： $(35×15)×\frac{7}{35}×\frac{2}{15}$ $6×\left(\frac{5}{6}-\frac{5}{8}\right)×8$
$=\left(35×\frac{7}{35}\right)×\left(15×\frac{2}{15}\right)$ $=6×\frac{5}{6}×8-6×\left(\frac{5}{8}×8\right)$
$=7×2$ $=40-30$
$=14$ $=10$

3. 解方程。
$\frac{1}{4}x+\frac{2}{3}x= 22$
$\frac{9}{10}x-\frac{1}{4}= \frac{1}{5}$

答案： $\frac{1}{4}x+\frac{2}{3}x=22$ $\frac{9}{10}x-\frac{1}{4}=\frac{1}{5}$
解：$\left(\frac{1}{4}+\frac{2}{3}\right)x=22$ 解：$\frac{9}{10}x=\frac{1}{5}+\frac{1}{4}$
$\frac{11}{12}x=22$ $\frac{9}{10}x=\frac{9}{20}$
$x=22÷\frac{11}{12}$ $x=\frac{9}{20}÷\frac{9}{10}$
$x=24$ $x=\frac{1}{2}$

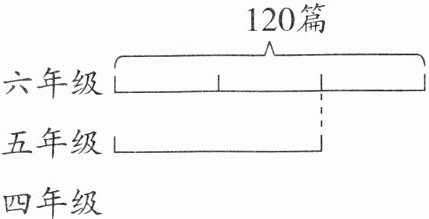
4. 新考法图文转换法 春风小学组织“书香校园读书月”征文活动,六年级上交了120篇作文,五年级上交的篇数是六年级的$\frac{2}{3}$,四年级上交的篇数是五年级的$\frac{3}{5}$。四年级上交了多少篇作文？(先把线段图补充完整,再解答)

答案：

$120×\frac{2}{3}×\frac{3}{5}=48$（篇）
答：四年级上交了48篇作文。
[点拨]连续求一个数的几分之几是多少，用乘法计算。先求出五年级上交的篇数，再用五年级上交的篇数乘$\frac{3}{5}$即为所求。

5. 秦始皇兵马俑是世界八大奇迹之一。秦始皇兵马俑博物馆去年十一黄金周第一天共接待游客6万人,第二天比第一天多接待了$\frac{1}{5}$。去年十一黄金周第二天共接待游客多少万人？

答案： $6×\left(1+\frac{1}{5}\right)=7.2$（万人）
答：去年十一黄金周第二天共接待游客7.2万人。

6. 某景区准备做120个长椅供游客休息,有$\frac{2}{5}$是木质座椅,$\frac{1}{3}$是石头座椅,其余是竹制座椅,竹制座椅有多少个？

答案： $120×\left(1-\frac{2}{5}-\frac{1}{3}\right)=32$（个）
答：竹制座椅有32个。
[点拨]把长椅总数看作单位“1”，用单位“1”减去木质座椅、石头座椅对应的分率，求出竹制座椅对应的分率，根据总量×分率=分量，求出竹制座椅的数量。

7. 垃圾分类有减少污染、变废为宝等好处。幸福里小区今年自觉参与垃圾分类的有560人,比去年增加了$\frac{2}{5}$,幸福里小区去年自觉参与垃圾分类的有多少人？

答案： $560÷\left(1+\frac{2}{5}\right)=400$（人）
答：幸福里小区去年自觉参与垃圾分类的有400人。
[点拨]根据题意，把去年自觉参与垃圾分类的人数看作单位"1”，则今年自觉参与垃圾分类的人数是去年的$\left(1+\frac{2}{5}\right)$，求去年自觉参与垃圾分类的人数，用除法计算。

8. 超市购进一批大米,上午卖出了全部的$\frac{2}{9}$,下午卖出的比全部的$\frac{1}{4}$多2吨,还剩36吨,超市购进大米多少吨？

答案： $(36+2)÷\left(1-\frac{2}{9}-\frac{1}{4}\right)=72$（吨）
答：超市购进大米72吨。
[点拨]把这批大米的总质量看作单位“1”，由“下午卖出的比全部的$\frac{1}{4}$多2吨，还剩36吨”，可以转化为若下午只卖出全部的$\frac{1}{4}$，则这批大米还剩$(36+2)$吨，对应的分率是$\left(1-\frac{2}{9}-\frac{1}{4}\right)$，用“对应数量÷对应分率”即可求出这批大米的总质量。