《2025年综合应用创新题典中点六年级数学上册北师大版》

1. 母题教材P16例题 太极图展现了一种互相的转化,相对统一的形式美。武当山上有一幅太极图(如图),它的半径是3 m,这幅太极图的面积是多少平方米？

答案： 3.14×3²=28.26(m²)
答:这幅太极图的面积是28.26m²。
【点拨】已知太极图的半径,根据圆的面积公式S=πr²,代入数据计算即可。

(1)一个圆形花坛的周长是6.28 m,这个花坛的半径是(1)m,面积是(3.14)$m^{2}$。

答案：
(1)1 3.14
根据圆的周长公式C=2πr,可得半径为6.28÷3.14÷2=1(m),再根据圆的面积公式S=πr²,可求出面积是3.14×1²=3.14(m²)。

(2)一个半圆形的周长是102.8 cm,这个半圆形的面积是( )$cm^{2}$。

答案：
(2)628 
根据半圆形周长=圆周长的一半+直径,进行逆算,求出半圆形的直径是102.8÷(3.14÷2+1)=40(cm),则半径是40÷2=20(cm)。所以这个半圆形的面积是3.14×20²÷2=628(cm²)。

3. 母题教材P16例题 北京天坛是中国现存最大的古代祭祀性建筑群。其中祈年殿的底部是周长约为75.36 m的圆,祈年殿的占地面积大约是多少平方米？

答案： 75.36÷3.14÷2=12(m) 3.14×12²=452.16(m²)
答:祈年殿的占地面积大约是452.16m²。
【点拨】先根据祈年殿的底部周长求出祈年殿的底部半径,再根据圆的面积公式S=πr²计算出其占地面积即可。

4. 新考法转化法在探究圆的面积公式时,典典将一个圆形纸片剪拼成一个近似的三角形(如图)。

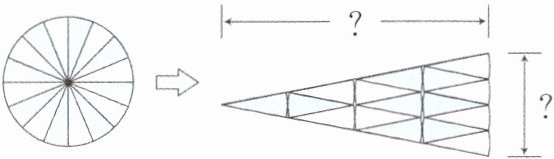
三角形的底相当于圆周长的($\frac{1}{4}$),高相当于半径的(4)倍,三角形的面积= 底×高×$\frac{1}{2}$= ($\frac{1}{4}$C)×(4r)×$\frac{1}{2}$= (πr²)= 圆的面积。

答案： $\frac{1}{4}$ 4 $\frac{1}{4}$C 4r πr²

5. 新题型数学文化题 我国古代数学名著《九章算术》方田章记载了这样一种求圆环面积的公式：“并中外周而半之,以径乘之为积步”,意思是将外圆和内圆的周长的平均数乘环的宽度可以得到环形的面积。利用这个公式求下面圆环的面积,并利用我们教材上计算圆环面积的方法验证结果是否正确。

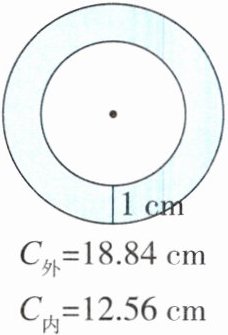
答案： (18.84+12.56)÷2×1=15.7(cm²)
18.84÷3.14÷2=3(cm) 12.56÷3.14÷2=2(cm)
3.14×(3²-2²)=15.7(cm²)
答:圆环的面积是15.7cm²,验证结果正确。
【点拨】理解《九章算术》中求圆环面积的方法是关键。先用给出的方法计算出圆环面积,再根据给出的周长分别求出外圆和内圆的半径,利用教材上学习的圆环面积公式S=π(R²-r²)求出圆环面积,然后验证结果是否正确。

6. 苏州园林有一扇景观窗,形状是外圆内方,另一扇景观窗的形状是外方内圆,这两扇窗户中圆的直径都是2 m,你能求出两扇窗户中正方形和圆的面积差分别是多少吗？

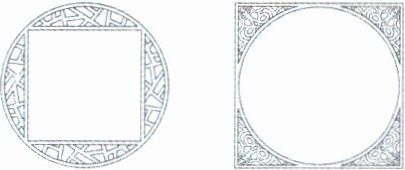
答案： 2÷2=1(m) 3.14×1²=3.14(m²)
3.14-1×1÷2×4=1.14(m²) 2×2-3.14=0.86(m²)
答:两扇窗户中正方形和圆的面积差分别是1.14m²和0.86m²。
【点拨】左图外面是圆,里面是正方形,则这扇窗户中正方形和圆的面积差=圆的面积-正方形的面积,其中正方形可以看作是4个相同的小等腰直角三角形,其直角边等于圆的半径。右图外面是正方形,里面是圆,则这扇窗户中正方形和圆的面积差=正方形的面积-圆的面积,其中正方形的边长等于圆的直径。

7. 如图,已知涂色部分的面积是$30cm^{2}$,这个圆环的面积是多少平方厘米？

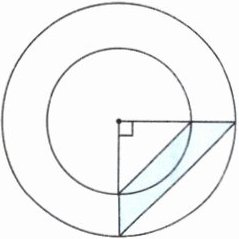
答案： 3.14×(30×2)=188.4(cm²)
答: 这个圆环的面积是188.4cm²。
【点拨】设外圆的半径为R cm,内圆的半径为r cm。观察题图可知,涂色部分的面积等于大三角形的面积减去小三角形的面积,根据三角形面积公式可得$\frac{1}{2}$R²-$\frac{1}{2}$r²=30,进而得到R²-r²=30×2,再将其整体代入环形面积公式求解即可。