《2025年暑假作业本大象出版社八年级数学人教版》

3. 将一次函数$y= \frac {1}{2}x$的图象向上平移2个单位长度,平移后,若$y＞0$,则$x$的取值范围是 (B)
A.$x＞4$
B.$x＞-4$
C.$x＞2$
D.$x＞-2$

答案： 3. B

4. 已知一个函数的函数值$y与自变量x$的几组对应值如下表,则这个函数的表达式可以是 (A)
| $x$ | …$$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $y$ | …$$ | $-2$ | $0$ | $2$ | $4$ | …$$ |
A.$y= 2x$
B.$y= x-1$
C.$y= \frac {2}{x}$
D.$y= x^{2}$

答案： 4. A

5. 定义:点$A(x,y)$为平面直角坐标系内的点,若满足$x= y$,则把点$A$叫做“平衡点”. 例如:$M(1,1),N(-2,-2)$都是“平衡点”. 当$-1≤x≤3$时,直线$y= 2x+m$上有“平衡点”,则$m$的取值范围是 (B)
A.$0≤m≤1$
B.$-3≤m≤1$
C.$-3≤m≤3$
D.$-1≤m≤0$

答案： 5. B

6. 函数$y= (m+2)x+m+4$中$y$随$x$的增大而减小,且图象交$y$轴于正半轴,则$m$的取值范围是$-4 ＜ m ＜ -2$.

答案： 6. $-4 ＜ m ＜ -2$

7. 在平面直角坐标系中,点$P(x_{0},y_{0})$到直线Ax+By+C= 0的距离公式为$d= \frac {|Ax_{0}+By_{0}+C|}{\sqrt {A^{2}+B^{2}}}$,则点$P(3,-3)$到直线$y= -\frac {2}{3}x+\frac {5}{3}$的距离为$\frac{8}{13}\sqrt{13}$.

答案： 7. $\frac{8}{13}\sqrt{13}$

8. 如图19-22,直线$y= 2x+4与x轴交于点A$,与$y轴交于点B$,点$D为OB$的中点,$□ OCDE的顶点C在x$轴上,顶点$E在直线AB$上,则$□ OCDE$的面积为2.

答案： 8. 2

9. 如图19-23,在平面直角坐标系中,点$A,B的坐标分别为(1,3),(n,3)$,若直线$y= 2x与线段AB$有公共点,则$n$的值可以为2(写出一个即可).

答案： 9. 答案不唯一，只要 $n \geq \frac{3}{2}$ 即可，如 2

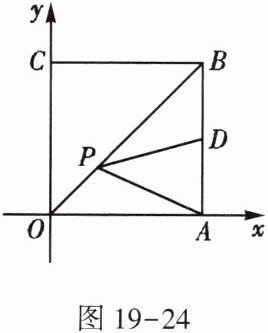
10. 如图19-24,在平面直角坐标系中,点$A,C分别在x$轴、$y$轴上,四边形$ABCO$是边长为4的正方形,点$D为AB$的中点,$P为OB$上的一个动点,连接$DP,AP$,当点$P满足DP+AP$的值最小时,直线$AP$的解析式为____.

答案：
10. $y = -2x + 8$ 提示：

∵ 四边形 $ABCO$ 是正方形，
∴ 点 $A$，$C$ 关于直线 $OB$ 对称。如图，连接 $CD$ 交 $OB$ 于点 $P$，连接 $PA$，$PD$，则此时 $DP + AP$ 的值最小。
∵ $OC = OA = AB = 4$，
∴ $C$ 的坐标为 $(0, 4)$，$A$ 的坐标为 $(4, 0)$。
∵ $D$ 为 $AB$ 的中点，
∴ $AD = \frac{1}{2}AB = 2$，
∴ $D$ 的坐标为 $(4, 2)$。设直线 $CD$ 的解析式为 $y = kx + b(k \neq 0)$，则 $\begin{cases}4k + b = 2, \\ b = 4.\end{cases}$ 解得 $\begin{cases}k = -\frac{1}{2}, \\ b = 4.\end{cases}$
∴ 直线 $CD$ 的解析式为 $y = -\frac{1}{2}x + 4$。
∵ 直线 $OB$ 的解析式为 $y = x$，联立 $\begin{cases}y = -\frac{1}{2}x + 4, \\ y = x\end{cases}$ 解得 $x = y = \frac{8}{3}$。
∴ $P$ 的坐标为 $(\frac{8}{3}, \frac{8}{3})$。设直线 $AP$ 的解析式为 $y = mx + n(m \neq 0)$，则 $\begin{cases}4m + n = 0, \\ \frac{8}{3}m + n = \frac{8}{3}\end{cases}$ 解得 $\begin{cases}m = -2, \\ n = 8\end{cases}$。
∴ 直线 $AP$ 的解析式为 $y = -2x + 8$。