《2025年暑假作业本大象出版社八年级数学人教版》

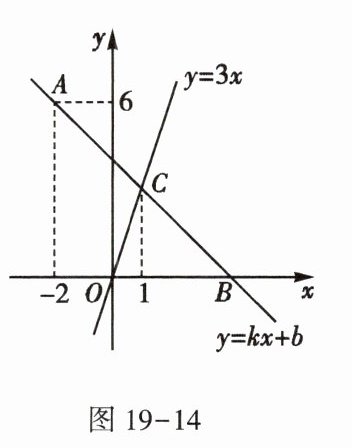
7. 如图19-14,在平面直角坐标系中,一次函数$y = kx + b的图象经过点A( - 2,6)$,且与$x轴相交于点B$,与正比例函数$y = 3x的图象相交于点C$,点$C的横坐标为1$.
(1) 求$k$,$b$的值；
(2) 请直接写出不等式$kx + b - 3x＞0$的解集；
(3) 若点$D在y$轴上,且满足$S_{\triangle BCD} = 2S_{\triangle BOC}$,求点$D$的坐标.

答案：
7.
(1) 当 $x = 1$ 时，$y = 3x = 3$，$\therefore$ 点 $C$ 的坐标为 $(1, 3)$. 将 $A(-2, 6)$，$C(1, 3)$ 代入 $y = kx + b$，得 $ \begin{cases} -2k + b = 6, \\ k + b = 3. \end{cases} $ 解得 $ \begin{cases} k = -1, \\ b = 4. \end{cases} $
(2) $x ＜ 1$.
(3) 由
(1) 知，直线 $AB: y = -x + 4$. 当 $y = 0$ 时，有 $-x + 4 = 0$. 解得 $x = 4$，$\therefore$ 点 $B$ 的坐标为 $(4, 0)$. 设点 $D$ 的坐标为 $(0, m)$，$\therefore$ 直线 $DB: y = -\frac{m}{4}x + m$. 过点 $C$ 作 $CE // y$ 轴，交 $BD$ 于点 $E$，则 $E(1, \frac{3}{4}m)$，$\therefore CE = |3 - \frac{3}{4}m|$，$\therefore S_{\triangle BCD} = S_{\triangle CED} + S_{\triangle CEB} = \frac{1}{2}CE \cdot OB = \frac{1}{2}|3 - \frac{3}{4}m| × 4 = 2|3 - \frac{3}{4}m|$. $\because S_{\triangle BCD} = 2S_{\triangle BOC}$，即 $2|3 - \frac{3}{4}m| = \frac{1}{2} × 4 × 3 × 2$，解得 $m = -4$ 或 $m = 12$，$\therefore$ 点 $D$ 的坐标为 $(0, -4)$ 或 $(0, 12)$.

1. 设点$A(a,b)是正比例函数y= -\frac {3}{2}x$图象上的任意一点,则下列等式一定成立的是 (D)
A.$2a+3b= 0$
B.$2a-3b= 0$
C.$3a-2b= 0$
D.$3a+2b= 0$

答案： D

2. 在同一平面直角坐标系中,一次函数$y= ax+a^{2}与y= a^{2}x+a$的图象可能是图 19-15 中的 (D)

答案： D