《2025年暑假作业本大象出版社八年级数学人教版》

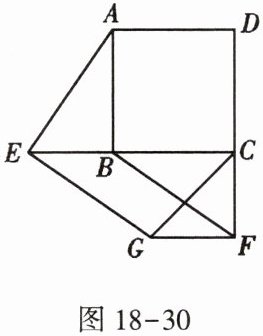
8. 如图18-30,$E$,$F分别是正方形ABCD的边CB$,$DC$延长线上的点,且$BE = CF$,过点$E作EG// BF$,交正方形外角的平分线$CG于点G$,连接$GF$.
求证：(1)$AE⊥BF$；
(2)四边形$BEGF$是平行四边形.

答案：

(1)
∵ 四边形ABCD是正方形，
∴ AB = BC，∠ABC = ∠BCD = 90°，
∴ ∠ABE = ∠BCF = 90°。在△ABE和△BCF中，$\left\{\begin{array}{l}AB = BC,\\\angle ABE = \angle BCF,\\BE = CF,\end{array}\right.$
∴ △ABE ≌ △BCF(SAS)，
∴ AE = BF，∠BAE = ∠CBF。
∵ EG//BF，
∴ ∠CBF = ∠CEG。
∵ ∠BAE + ∠BEA = 90°，
∴ ∠CEG + ∠BEA = 90°，
∴ AE⊥EG，
∴ AE⊥BF。
(2)延长AB至点P，使BP = BE，连接EP，如图所示，则AP = CE，∠EBP = 90°，∠P = 45°。
∵ CG为正方形ABCD外角的平分线，
∴ ∠ECG = 45°，
∴ ∠P = ∠ECG。由
(1)，得∠BAE = ∠CEG。在△APE和△ECG中，$\left\{\begin{array}{l}\angle P = \angle ECG,\\AP = CE,\\\angle BAE = \angle CEG,\end{array}\right.$
∴ △APE ≌ △ECG(ASA)，
∴ AE = EG。
∵ AE = BF，
∴ EG = BF。
∵ EG//BF，
∴ 四边形BEGF是平行四边形。
　　　　　　　　　　　　　

1. 在平面直角坐标系中,$□ ABCD的顶点A,B,C的坐标分别是(0,0),(3,0),(4,2)$,则顶点$D$的坐标为(C)
A.$(7,2)$
B.$(5,4)$
C.$(1,2)$
D.$(2,1)$

答案： C

2. 在$□ ABCD$中,$AB= 3,BC= 4$,当$□ ABCD$的面积最大时,有下列结论:①$AC= 5$;②$∠A+∠C= 180^{\circ }$;③$AC⊥BD$;④$AC= BD$.其中正确的是(B)
A.①②③
B.①②④
C.②③④
D.①③④

答案： B

3. 如图18-31,在菱形$ABCD$中,$∠D= 150^{\circ }$,则$∠1$的度数为(D)
A.$30^{\circ }$
B.$25^{\circ }$
C.$20^{\circ }$
D.$15^{\circ }$

答案： D

4. 如图18-32,在$□ ABCD$中,$AB= 8$,$E是AB$上一点,$AE= 3$,连接$DE$,过点$C作CF// DE$,交$AB的延长线于点F$,则$BF$的长为(C)
A.5
B.4
C.3
D.2

答案： C