知识回顾
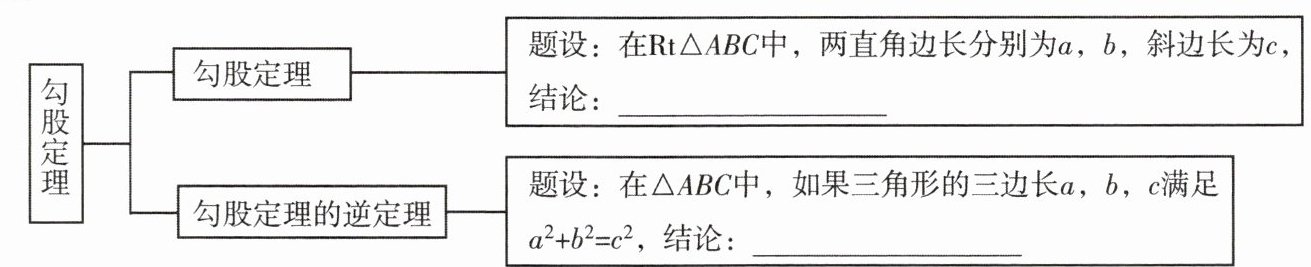

$a^{2}+b^{2}=c^{2}$;$\triangle ABC$是直角三角形
答案:
【解析】:勾股定理是在直角三角形中,两直角边的平方和等于斜边的平方;勾股定理的逆定理是如果三角形三边满足两短边的平方和等于最长边的平方,那么这个三角形是直角三角形。
【答案】:$a^{2}+b^{2}=c^{2}$;$\triangle ABC$是直角三角形
【答案】:$a^{2}+b^{2}=c^{2}$;$\triangle ABC$是直角三角形
勾股定理
直角三角形的两条直角边的平方和等于斜边的平方,即若直角三角形两直角边为$a$、$b$,斜边为$c$,则$a^{2}+b^{2}=c^{2}$
答案:
直角三角形的两条直角边的平方和等于斜边的平方,即若直角三角形两直角边为$a$、$b$,斜边为$c$,则$a^{2}+b^{2}=c^{2}$
一、勾股定理
一、
答案:
一、
1. 在平面直角坐标系中,点$P(2,-3)$到原点的距离是(
A.$\sqrt{5}$
B.$\sqrt{11}$
C.$\sqrt{13}$
D.$2$
C
)A.$\sqrt{5}$
B.$\sqrt{11}$
C.$\sqrt{13}$
D.$2$
答案:
1. C
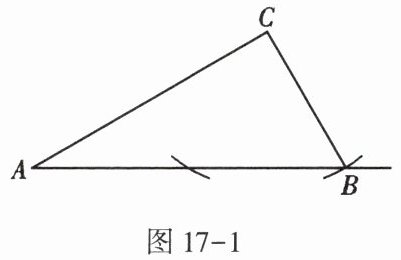
2. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等. 如已知$\triangle ABC$中,$\angle A= 30^{\circ}$,$AC= 3$,$\angle A所对的边为\sqrt{3}$,满足已知条件的三角形有两个(我们发现其中如图17-1的$\triangle ABC$是一个直角三角形),则满足已知条件的三角形的第三边长为( )
A.$2\sqrt{3}$
B.$2\sqrt{3}-3$
C.$2\sqrt{3}或\sqrt{3}$
D.$2\sqrt{3}或2\sqrt{3}-3$

A.$2\sqrt{3}$
B.$2\sqrt{3}-3$
C.$2\sqrt{3}或\sqrt{3}$
D.$2\sqrt{3}或2\sqrt{3}-3$
答案:
2. C 提示:如图,$CD=CB$,作$CH⊥AB$于点 H,$\therefore DH=BH.\because ∠A=30^{\circ },\therefore CH=\frac {1}{2}AC=\frac {3}{2},AH=\sqrt {3}CH=\frac {3}{2}\sqrt {3}$. 在$Rt△CBH$中,由勾股定理,得$BH=\sqrt {BC^{2}-CH^{2}}=\sqrt {3-\frac {9}{4}}=\frac {\sqrt {3}}{2}$, $\therefore AB=AH+BH=\frac {3\sqrt {3}}{2}+\frac {\sqrt {3}}{2}=2\sqrt {3},AD=AH-DH=\frac {3\sqrt {3}}{2}-\frac {\sqrt {3}}{2}=\sqrt {3}$. 故满足已知条件的三角形的第三边长为$2\sqrt {3}$或$\sqrt {3}$.

2. C 提示:如图,$CD=CB$,作$CH⊥AB$于点 H,$\therefore DH=BH.\because ∠A=30^{\circ },\therefore CH=\frac {1}{2}AC=\frac {3}{2},AH=\sqrt {3}CH=\frac {3}{2}\sqrt {3}$. 在$Rt△CBH$中,由勾股定理,得$BH=\sqrt {BC^{2}-CH^{2}}=\sqrt {3-\frac {9}{4}}=\frac {\sqrt {3}}{2}$, $\therefore AB=AH+BH=\frac {3\sqrt {3}}{2}+\frac {\sqrt {3}}{2}=2\sqrt {3},AD=AH-DH=\frac {3\sqrt {3}}{2}-\frac {\sqrt {3}}{2}=\sqrt {3}$. 故满足已知条件的三角形的第三边长为$2\sqrt {3}$或$\sqrt {3}$.

3. 如图 17-2,在 Rt△ABC中,∠ACB = 90°,AD平分∠BAC 与 BC相交于点D.若BD=4,CD=2,则AB的长是
4√3
。
答案:
3.$4\sqrt {3}$
查看更多完整答案,请扫码查看


