《2025年暑假作业本大象出版社八年级数学人教版》

11. 如图18-37,四边形$ABCD$是菱形,$AE⊥BC于点E$,$AF⊥CD于点F$.
(1)求证:$\triangle ABE\cong \triangle ADF$;
(2)若$AE= 4,CF= 2$,求菱形的边长为5.

答案：
(1)
∵ 四边形 $ A B C D $ 是菱形，
∴ $ A B = B C = C D = A D $，$ \angle B = \angle D $。
∵ $ A E \perp B C $，$ A F \perp C D $，
∴ $ \angle A E B = \angle A F D = 90 ^ { \circ } $。在 $ \triangle A B E $ 和 $ \triangle A D F $ 中，
$\left\{ \begin{array} { l } { \angle A E B = \angle A F D } \\ { \angle B = \angle D } \\ { A B = A D } \end{array} \right.$
∴ $ \triangle A B E \cong \triangle A D F ( A A S ) $。
(2) 设菱形的边长为 $ x $。
∵ $ A B = C D = x $，$ C F = 2 $，
∴ $ D F = x - 2 $。
∵ $ \triangle A B E \cong \triangle A D F $，
∴ $ B E = D F = x - 2 $。在 $ \mathrm { Rt } \triangle A B E $ 中，根据勾股定理，得 $ A E ^ { 2 } + B E ^ { 2 } = A B ^ { 2 } $，即 $ 4 ^ { 2 } + ( x - 2 ) ^ { 2 } = x ^ { 2 } $，解得 $ x = 5 $，
∴ 菱形的边长是 5。

12. 在矩形$ABCD$中,$BD$是对角线,$AE⊥BD于点E$,$CF⊥BD于点F$.

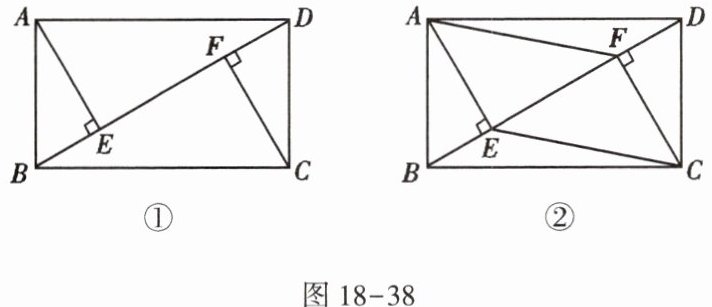
(1)如图18-38①,求证:$AE= CF$;
(2)如图18-38②,当$∠ADB= 30^{\circ }$时,连接$AF,CE$,在不添加任何辅助线的情况下,请直接写出图18-38②中四个三角形,使写出的每个三角形的面积都等于矩形$ABCD面积的\frac {1}{8}$.
(1) ∵ 四边形 $ A B C D $ 是矩形，∴ $ A B = C D $，$ A B // C D $，$ A D // B C $，∴ $ \angle A B E = \angle C D F $。∵ $ A E \perp B D $ 于点 $ E $，$ C F \perp B D $ 于点 $ F $，∴ $ \angle A E B = \angle C F D = 90 ^ { \circ } $。在 $ \triangle A B E $ 和 $ \triangle C D F $ 中，
$\left\{ \begin{array} { l } { \angle A B E = \angle C D F } \\ { \angle A E B = \angle C F D } \\ { A B = C D } \end{array} \right.$
∴ $ \triangle A B E \cong \triangle C D F ( A A S ) $，∴ $ A E = C F $。
(2) $\triangle ABE$，$\triangle CDF$，$\triangle BCE$，$\triangle ADF$都等于矩形$ABCD$面积的$\frac {1}{8}$。

答案：
(1)
∵ 四边形 $ A B C D $ 是矩形，
∴ $ A B = C D $，$ A B // C D $，$ A D // B C $，
∴ $ \angle A B E = \angle C D F $。
∵ $ A E \perp B D $ 于点 $ E $，$ C F \perp B D $ 于点 $ F $，
∴ $ \angle A E B = \angle C F D = 90 ^ { \circ } $。在 $ \triangle A B E $ 和 $ \triangle C D F $ 中，
$\left\{ \begin{array} { l } { \angle A B E = \angle C D F } \\ { \angle A E B = \angle C F D } \\ { A B = C D } \end{array} \right.$
∴ $ \triangle A B E \cong \triangle C D F ( A A S ) $，
∴ $ A E = C F $。
(2) $ \triangle A B E $，$ \triangle C D F $，$ \triangle B C E $，$ \triangle A D F $ 都等于矩形 $ A B C D $ 面积的 $ \frac { 1 } { 8 } $。提示：
∵ $ A D // B C $，
∴ $ \angle C B D = \angle A D B = 30 ^ { \circ } $。
∵ $ \angle A B C = 90 ^ { \circ } $，
∴ $ \angle A B E = 60 ^ { \circ } $。
∵ $ A E \perp B D $，
∴ $ \angle B A E = 30 ^ { \circ } $，
∴ $ B E = \frac { 1 } { 2 } A B $，$ A E = \frac { 1 } { 2 } A D $，
∴ $ S _ { \triangle A B E } = \frac { 1 } { 2 } B E × A E = \frac { 1 } { 2 } × \frac { 1 } { 2 } A B × \frac { 1 } { 2 } A D = \frac { 1 } { 8 } A B × A D = \frac { 1 } { 8 } S _ { \text { 矩形 } A B C D } $。
∵ $ \triangle A B E \cong \triangle C D F $，
∴ $ S _ { \triangle C D F } = \frac { 1 } { 8 } S _ { \text { 矩形 } A B C D } $。作 $ E G \perp B C $ 于点 $ G $，
∵ $ \angle C B D = 30 ^ { \circ } $，
∴ $ E G = \frac { 1 } { 2 } B E = \frac { 1 } { 2 } × \frac { 1 } { 2 } A B = \frac { 1 } { 4 } A B $，
∴ $ S _ { \triangle B C E } = \frac { 1 } { 2 } B C × E G = \frac { 1 } { 2 } B C × \frac { 1 } { 4 } A B = \frac { 1 } { 8 } B C × A B = \frac { 1 } { 8 } S _ { \text { 矩形 } A B C D } $。同理，$ S _ { \triangle A D F } = \frac { 1 } { 8 } S _ { \text { 矩形 } A B C D } $。