9. 如图18-48,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 5$,$AC = 3$,$P为边AB$上一动点(且点$P不与点A$,$B$重合),$PE\perp BC于点E$,$PF\perp AC于点F$,点$M为EF$的中点,则$PM$的最小值为______
$\frac{6}{5}$
.
答案:
$ \frac{6}{5} $ 提示:在 $ Rt\triangle ABC $ 中,
∵ $ \angle ACB = 90^{\circ} $,$ AB = 5 $,$ AC = 3 $,
∴ $ BC = \sqrt{5^{2} - 3^{2}} = 4 $。
∵ $ PE \perp BC $ 于点 E,$ PF \perp AC $ 于点 F,
∴ $ \angle PEC = \angle PFC = \angle EPF = 90^{\circ} $,
∴ 四边形 CEPF 是矩形。
∵ M 是 EF 的中点,
∴ 延长 PM 经过点 C,
∴ $ EF = CP $,$ PM = \frac{1}{2}EF = \frac{1}{2}PC $,当 $ PC \perp AB $ 时,$ PC = \frac{4 × 3}{5} = \frac{12}{5} $,
∴ PM 的最小值为 $ \frac{6}{5} $。
∵ $ \angle ACB = 90^{\circ} $,$ AB = 5 $,$ AC = 3 $,
∴ $ BC = \sqrt{5^{2} - 3^{2}} = 4 $。
∵ $ PE \perp BC $ 于点 E,$ PF \perp AC $ 于点 F,
∴ $ \angle PEC = \angle PFC = \angle EPF = 90^{\circ} $,
∴ 四边形 CEPF 是矩形。
∵ M 是 EF 的中点,
∴ 延长 PM 经过点 C,
∴ $ EF = CP $,$ PM = \frac{1}{2}EF = \frac{1}{2}PC $,当 $ PC \perp AB $ 时,$ PC = \frac{4 × 3}{5} = \frac{12}{5} $,
∴ PM 的最小值为 $ \frac{6}{5} $。
10. 如图18-49,在矩形$ABCD$中,$AD = 4$,$P是直线AD$上一动点,若满足$\triangle PBC是等腰三角形的点P$有且只有3个,则$AB$的长为
4
.
答案:
4
11. 如图18-50,已知四边形$ABCD$是正方形,$G为线段AD$上任意一点,$CE\perp BG于点E$,$DF\perp CE于点F$.求证:$DF = BE + EF$.
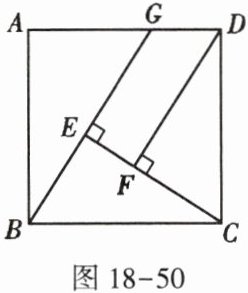
证明:∵ 四边形 ABCD 是正方形,∴ $ BC = CD $,$ \angle BCD = 90^{\circ} $。∵ $ CE \perp BG $,$ DF \perp CE $,∴ $ \angle BEC = \angle CFD = 90^{\circ} $,∴ $ \angle BCE + \angle CBE = 90^{\circ} = \angle BCE + \angle DCF $。∴ $ \angle CBE = \angle DCF $。在 $ \triangle CBE $ 和 $ \triangle DCF $ 中,$ \left\{ \begin{array}{l} \angle CBE = \angle DCF, \\ \angle BEC = \angle CFD, \\ BC = CD, \end{array} \right. $ ∴ $ \triangle CBE \cong \triangle DCF $(

证明:∵ 四边形 ABCD 是正方形,∴ $ BC = CD $,$ \angle BCD = 90^{\circ} $。∵ $ CE \perp BG $,$ DF \perp CE $,∴ $ \angle BEC = \angle CFD = 90^{\circ} $,∴ $ \angle BCE + \angle CBE = 90^{\circ} = \angle BCE + \angle DCF $。∴ $ \angle CBE = \angle DCF $。在 $ \triangle CBE $ 和 $ \triangle DCF $ 中,$ \left\{ \begin{array}{l} \angle CBE = \angle DCF, \\ \angle BEC = \angle CFD, \\ BC = CD, \end{array} \right. $ ∴ $ \triangle CBE \cong \triangle DCF $(
AAS
),∴ $ CF = BE $,$ CE = DF $。∵ $ CE = EF + CF $,∴ $ DF = BE + EF $。
答案:
∵ 四边形 ABCD 是正方形,
∴ $ BC = CD $,$ \angle BCD = 90^{\circ} $。
∵ $ CE \perp BG $,$ DF \perp CE $,
∴ $ \angle BEC = \angle CFD = 90^{\circ} $,
∴ $ \angle BCE + \angle CBE = 90^{\circ} = \angle BCE + \angle DCF $。
∴ $ \angle CBE = \angle DCF $。在 $ \triangle CBE $ 和 $ \triangle DCF $ 中,$ \left\{ \begin{array}{l} \angle CBE = \angle DCF, \\ \angle BEC = \angle CFD, \\ BC = CD, \end{array} \right. $
∴ $ \triangle CBE \cong \triangle DCF (AAS) $,
∴ $ CF = BE $,$ CE = DF $。
∵ $ CE = EF + CF $,
∴ $ DF = BE + EF $。
∵ 四边形 ABCD 是正方形,
∴ $ BC = CD $,$ \angle BCD = 90^{\circ} $。
∵ $ CE \perp BG $,$ DF \perp CE $,
∴ $ \angle BEC = \angle CFD = 90^{\circ} $,
∴ $ \angle BCE + \angle CBE = 90^{\circ} = \angle BCE + \angle DCF $。
∴ $ \angle CBE = \angle DCF $。在 $ \triangle CBE $ 和 $ \triangle DCF $ 中,$ \left\{ \begin{array}{l} \angle CBE = \angle DCF, \\ \angle BEC = \angle CFD, \\ BC = CD, \end{array} \right. $
∴ $ \triangle CBE \cong \triangle DCF (AAS) $,
∴ $ CF = BE $,$ CE = DF $。
∵ $ CE = EF + CF $,
∴ $ DF = BE + EF $。
12. 如图18-51,在四边形$ABCD$中,$\angle A = \angle ABC = 90^{\circ}$,$AD = 1$,$BC = 3$,$E是边CD$的中点,连接$BE并延长与AD的延长线相交于点F$.
(1) 求证:四边形$BDFC$是平行四边形;
(2) 若$\triangle BCD$是等腰三角形,求四边形$BDFC$的面积.

(1) 求证:四边形$BDFC$是平行四边形;
(2) 若$\triangle BCD$是等腰三角形,求四边形$BDFC$的面积.

答案:
(1)
∵ $ \angle A = \angle ABC = 90^{\circ} $,
∴ $ BC // AD $,
∴ $ \angle CBE = \angle DFE $。又
∵ E 是边 CD 的中点,
∴ $ CE = DE $。在 $ \triangle BEC $ 和 $ \triangle FED $ 中,$ \left\{ \begin{array}{l} \angle CBE = \angle DFE, \\ \angle BEC = \angle FED, \\ CE = DE, \end{array} \right. $
∴ $ \triangle BEC \cong \triangle FED (AAS) $,
∴ $ BE = FE $,
∴ 四边形 BDFC 是平行四边形。
(2) ① 当 $ BC = BD = 3 $ 时,由勾股定理,得 $ AB = \sqrt{BD^{2} - AD^{2}} = \sqrt{3^{2} - 1^{2}} = 2\sqrt{2} $,所以四边形 BDFC 的面积为 $ 3 × 2\sqrt{2} = 6\sqrt{2} $。
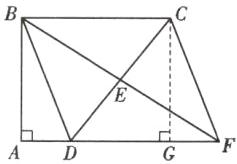
② 当 $ BC = CD = 3 $ 时,过点 C 作 $ CG \perp AF $ 于点 G,则四边形 AGCB 是矩形,
∴ $ AG = BC = 3 $,
∴ $ DG = AG - AD = 3 - 1 = 2 $,由勾股定理,得 $ CG = \sqrt{CD^{2} - DG^{2}} = \sqrt{3^{2} - 2^{2}} = \sqrt{5} $,
∴ 四边形 BDFC 的面积为 $ 3 × \sqrt{5} = 3\sqrt{5} $。③ 当 $ BD = CD $ 时,BC 边上的中线应该与 BC 垂直,从而得到 $ BC = 2AD = 2 $,与已知 $ BC = 3 $ 矛盾,故此时不成立。综上所述,四边形 BDFC 的面积是 $ 6\sqrt{2} $ 或 $ 3\sqrt{5} $。
(1)
∵ $ \angle A = \angle ABC = 90^{\circ} $,
∴ $ BC // AD $,
∴ $ \angle CBE = \angle DFE $。又
∵ E 是边 CD 的中点,
∴ $ CE = DE $。在 $ \triangle BEC $ 和 $ \triangle FED $ 中,$ \left\{ \begin{array}{l} \angle CBE = \angle DFE, \\ \angle BEC = \angle FED, \\ CE = DE, \end{array} \right. $
∴ $ \triangle BEC \cong \triangle FED (AAS) $,
∴ $ BE = FE $,
∴ 四边形 BDFC 是平行四边形。
(2) ① 当 $ BC = BD = 3 $ 时,由勾股定理,得 $ AB = \sqrt{BD^{2} - AD^{2}} = \sqrt{3^{2} - 1^{2}} = 2\sqrt{2} $,所以四边形 BDFC 的面积为 $ 3 × 2\sqrt{2} = 6\sqrt{2} $。

② 当 $ BC = CD = 3 $ 时,过点 C 作 $ CG \perp AF $ 于点 G,则四边形 AGCB 是矩形,
∴ $ AG = BC = 3 $,
∴ $ DG = AG - AD = 3 - 1 = 2 $,由勾股定理,得 $ CG = \sqrt{CD^{2} - DG^{2}} = \sqrt{3^{2} - 2^{2}} = \sqrt{5} $,
∴ 四边形 BDFC 的面积为 $ 3 × \sqrt{5} = 3\sqrt{5} $。③ 当 $ BD = CD $ 时,BC 边上的中线应该与 BC 垂直,从而得到 $ BC = 2AD = 2 $,与已知 $ BC = 3 $ 矛盾,故此时不成立。综上所述,四边形 BDFC 的面积是 $ 6\sqrt{2} $ 或 $ 3\sqrt{5} $。
查看更多完整答案,请扫码查看


