《2025年暑假作业本大象出版社八年级数学人教版》

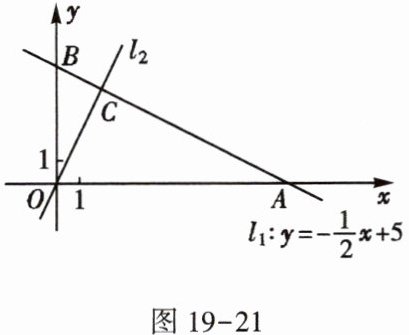
13. 如图 19-21,在平面直角坐标系中,一次函数$y= -\frac {1}{2}x+5的图象l_{1}$分别与 x,y 轴交于 A,B 两点,正比例函数的图象$l_{2}与l_{1}交于点C(m,4)$.

(1)求 m 的值及$l_{2}$的解析式；
m 的值为2，$l_{2}$的解析式为$y=2x$。
(2)求$S_{△AOC}-S_{△BOC}$的值；
值为15。
(3)一次函数$y= kx+1的图象为l_{3}$,且$l_{1},l_{2},l_{3}$不能围成三角形,直接写出 k 的值.
k 的值为$\frac{3}{2}$或2或$-\frac{1}{2}$。

答案：
(1) 把 $C(m, 4)$ 代入一次函数 $y = -\frac{1}{2}x + 5$，得 $4 = -\frac{1}{2}m + 5$，解得 $m = 2$，$\therefore C$ 的坐标为 $(2, 4)$。设 $l_2$ 的解析式为 $y = ax(a \neq 0)$，则 $4 = 2a$，解得 $a = 2$，$\therefore l_2$ 的解析式为 $y = 2x$。
(2) 过点 $C$ 作 $CD \perp AO$ 于点 $D$，$CE \perp BO$ 于点 $E$，则 $CD = 4$，$CE = 2$。对于 $y = -\frac{1}{2}x + 5$：令 $x = 0$，则 $y = 5$；令 $y = 0$，则 $x = 10$。$\therefore A$ 的坐标为 $(10, 0)$，$B$ 的坐标为 $(0, 5)$，$\therefore AO = 10$，$BO = 5$，$\therefore S_{\triangle AOC} - S_{\triangle BOC} = \frac{1}{2} × 10 × 4 - \frac{1}{2} × 5 × 2 = 20 - 5 = 15$。
(3) $\because$ 一次函数 $y = kx + 1$ 的图象为 $l_3$，且 $l_1$，$l_2$，$l_3$ 不能围成三角形，$\therefore$ 当 $l_3$ 经过点 $C(2, 4)$ 时，$k = \frac{3}{2}$；当 $l_2$ 与 $l_3$ 平行时，$k = 2$；当 $l_1$ 与 $l_3$ 平行时，$k = -\frac{1}{2}$。故 $k$ 的值为 $\frac{3}{2}$ 或 2 或 $-\frac{1}{2}$。

1. 函数$y= \frac {x}{\sqrt {x+3}}+\frac {1}{x-1}$的自变量x的取值范围是 (B)
A.$x≠-3且x≠1$
B.$x＞-3且x≠1$
C.$x＞-3$
D.$x≥-3且x≠1$

答案： 1. B

2. 若一次函数$y= (k-2)x+1的函数值y随x$的增大而增大,则 (B)
A.$k＜2$
B.$k＞2$
C.$k＞0$
D.$k＜0$

答案： 2. B