《2025年暑假作业本大象出版社八年级数学人教版》

1. 若一次函数$y = kx + b$($k$,$b$为常数,且$k≠0$)的图象经过点$A(0, - 1)$,$B(1,1)$,则不等式$kx + b＞1$的解集为(D)
A.$x＞0$
B.$x＜0$
C.$x＜1$
D.$x＞1$

答案： 1. D

2. 如图19-10,在平面直角坐标系中,$M是直线y = - x$上的动点,过点$M作MN⊥x$轴,交直线$y = x于点N$,当$MN≤8$时,设点$M的横坐标为m$,则$m$的取值范围为$-4 \leq m \leq 4$.

答案： 2. $-4 \leq m \leq 4$

3. 根据图象19-11所示,可得关于$x的不等式kx＞-x + 3$的解集是$x ＞ 1$.

答案： 3. $x ＞ 1$

4. 如图19-12,直线$y = kx + b过A( - 1,2)$,$B( - 2,0)$两点,则$0≤kx + b≤ - 2x$的解集为$-2 \leq x \leq -1$.

答案： 4. $-2 \leq x \leq -1$

5. 已知直线$y = 2x - b经过点(1, - 1)$,求关于$x的不等式2x - b≥0$的解集.

答案： 5. 直线 $y = 2x - b$ 经过点 $(1, -1)$，$\therefore -1 = 2 × 1 - b$，$\therefore b = 3$，$\therefore$ 不等式为 $2x - 3 \geq 0$，解得 $x \geq \frac{3}{2}$.

6. 如图19-13,已知直线$y = kx + 5交x轴于点A$,交$y轴于点B$,且点$A的坐标为(5,0)$,直线$y = 2x - 4与x轴交于点D$,与直线$AB相交于点C$.

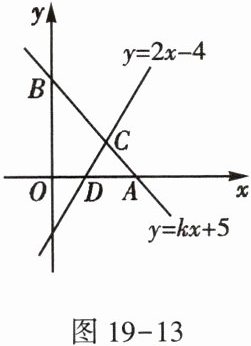
(1) 求点$C$的坐标；(3, 2)
(2) 根据图象,写出关于$x的不等式2x - 4＞kx + 5$的解集；x＞3
(3) 求$\triangle ADC$的面积.3

答案： 6.
(1) $\because$ 直线 $y = kx + 5$ 经过点 $A(5, 0)$，$\therefore 5k + 5 = 0$. 解得 $k = -1$. $\therefore$ 直线 $AB$ 的解析式为 $y = -x + 5$. 联立方程组 $ \begin{cases} y = -x + 5, \\ y = 2x - 4, \end{cases} $ 解得 $ \begin{cases} x = 3, \\ y = 2. \end{cases} $ $\therefore$ 点 $C$ 的坐标为 $(3, 2)$.
(2) 观察函数图象，可知当 $x ＞ 3$ 时，直线 $y = 2x - 4$ 在直线 $y = -x + 5$ 的上方，$\therefore$ 不等式 $2x - 4 ＞ kx + 5$ 的解集为 $x ＞ 3$.
(3) 把 $y = 0$ 代入 $y = 2x - 4$，得 $2x - 4 = 0$. 解得 $x = 2$. $\therefore D$ 的坐标为 $(2, 0)$. 又 $\because A$ 的坐标为 $(5, 0)$，$\therefore AD = 3$. 又 $\because C$ 的坐标为 $(3, 2)$，$\therefore S_{\triangle ADC} = \frac{1}{2} × 3 × 2 = 3$.