7. 如图18-24,在四边形$ABCD$中,$BC = CD$,$∠C = 2∠BAD$,$O是四边形ABCD$内一点,且$OA = OB = OD$.
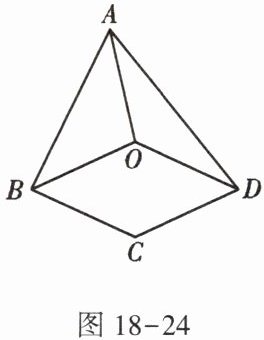
求证:(1)$∠BOD = ∠C$;
(2)四边形$OBCD$是菱形.

求证:(1)$∠BOD = ∠C$;
(2)四边形$OBCD$是菱形.
答案:
(1)延长AO到点E,
∵ OA = OB,
∴ ∠ABO = ∠BAO。又
∵ ∠BOE = ∠ABO + ∠BAO,
∴ ∠BOE = 2∠BAO,同理∠DOE = 2∠DAO,
∴ ∠BOE + ∠DOE = 2∠BAO + 2∠DAO = 2(∠BAO + ∠DAO),即∠BOD = 2∠BAD。又
∵ ∠C = 2∠BAD,
∴ ∠BOD = ∠C。
(2)连接OC,
∵ BC = CD,OB = OD,OC = OC,
∴ △OBC ≌ △ODC,
∴ ∠BOC = ∠DOC,∠BCO = ∠DCO。
∵ ∠BOD = ∠BOC + ∠DOC,∠BCD = ∠BCO + ∠DCO,
∴ ∠BOC = $\frac{1}{2}$∠BOD,∠BCO = $\frac{1}{2}$∠BCD。又
∵ ∠BOD = ∠BCD,
∴ ∠BOC = ∠BCO,
∴ OB = BC。又
∵ OB = OD,BC = CD,
∴ OB = BC = CD = OD,
∴ 四边形OBCD是菱形。
(1)延长AO到点E,
∵ OA = OB,
∴ ∠ABO = ∠BAO。又
∵ ∠BOE = ∠ABO + ∠BAO,
∴ ∠BOE = 2∠BAO,同理∠DOE = 2∠DAO,
∴ ∠BOE + ∠DOE = 2∠BAO + 2∠DAO = 2(∠BAO + ∠DAO),即∠BOD = 2∠BAD。又
∵ ∠C = 2∠BAD,
∴ ∠BOD = ∠C。
(2)连接OC,
∵ BC = CD,OB = OD,OC = OC,
∴ △OBC ≌ △ODC,
∴ ∠BOC = ∠DOC,∠BCO = ∠DCO。
∵ ∠BOD = ∠BOC + ∠DOC,∠BCD = ∠BCO + ∠DCO,
∴ ∠BOC = $\frac{1}{2}$∠BOD,∠BCO = $\frac{1}{2}$∠BCD。又
∵ ∠BOD = ∠BCD,
∴ ∠BOC = ∠BCO,
∴ OB = BC。又
∵ OB = OD,BC = CD,
∴ OB = BC = CD = OD,
∴ 四边形OBCD是菱形。
1. 如图18-25,$O为正方形ABCD对角线AC$的中点,$\triangle ACE$为等边三角形. 若$AB = 2$,则$OE$的长度为(
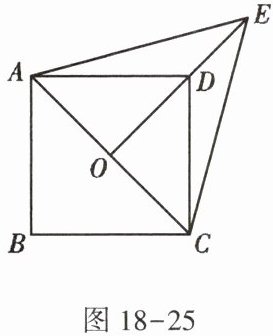
A.$\frac{\sqrt{6}}{2}$
B.$\sqrt{6}$
C.$2\sqrt{2}$
D.$2\sqrt{3}$
B
)
A.$\frac{\sqrt{6}}{2}$
B.$\sqrt{6}$
C.$2\sqrt{2}$
D.$2\sqrt{3}$
答案:
B
2. 四边形$ABCD$是菱形,添加一个条件:
∠BAD = 90°
,可使它成为正方形.
答案:
答案不唯一,如:∠BAD = 90°
3. 如果一个四边形既是菱形又是矩形,那么它一定是
正方形
.
答案:
正方形
4. 如图18-26,菱形$ABCD的面积为120\ cm^{2}$,正方形$AECF的面积为72\ cm^{2}$,则菱形的边长为
$2\sqrt{34}$
(结果中如有根号,请保留根号).
答案:
$2\sqrt{34}$
5. 如图18-27,正方形$ABCD$的边长为8,点$E是CD$的中点,$HG垂直平分AE且分别交AE$,$BC于点H$,$G$,则$BG = $______.
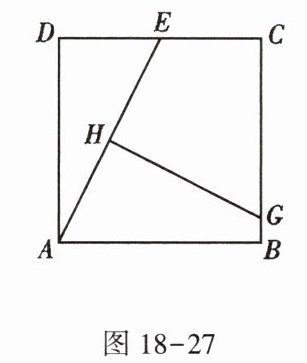

答案:
1 提示:连接AG,EG。
∵ E是CD的中点,
∴ DE = CE = 4。设CG = x,则BG = 8 - x。在Rt△ABG和Rt△GCE中,根据勾股定理,得AB² + BG² = AG² = EG² = CE² + CG²,
∴ 8² + (8 - x)² = 4² + x²,解得x = 7,
∴ BG = BC - CG = 8 - 7 = 1。

1 提示:连接AG,EG。
∵ E是CD的中点,
∴ DE = CE = 4。设CG = x,则BG = 8 - x。在Rt△ABG和Rt△GCE中,根据勾股定理,得AB² + BG² = AG² = EG² = CE² + CG²,
∴ 8² + (8 - x)² = 4² + x²,解得x = 7,
∴ BG = BC - CG = 8 - 7 = 1。

查看更多完整答案,请扫码查看


