《2025年暑假作业本大象出版社八年级数学人教版》

12. 如图17-25,在$△ABC$中,内角$∠A,∠B,∠C$所对的边分别为a,b,c.

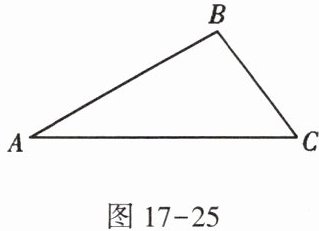
(1)若$a= 6,b= 8,c= 12$,请直接写出$∠A+∠B与∠C$的大小关系:∠A + ∠B ＜ ∠C;
(2)若$\frac {a}{a-b+c}= \frac {\frac {1}{2}(a+b+c)}{c}$,求证:$△ABC$是直角三角形.
证明:∵ $\frac{a}{a - b + c} = \frac{\frac{1}{2}(a + b + c)}{c}$，∴ $ac = \frac{1}{2}(a + b + c)(a - b + c) = \frac{1}{2}[(a + c) + b][(a + c) - b] = \frac{1}{2}[(a + c)^2 - b^2] = \frac{1}{2}[(a^2 + 2ac + c^2) - b^2]$，∴ 2ac = a² + 2ac + c² - b²，∴ a² + c² = b²，∴ △ABC 是直角三角形.

答案：
(1) ∠A + ∠B ＜ ∠C。
(2)
∵ $\frac{a}{a - b + c} = \frac{\frac{1}{2}(a + b + c)}{c}$，
∴ $ac = \frac{1}{2}(a + b + c)(a - b + c) = \frac{1}{2}[(a + c) + b][(a + c) - b] = \frac{1}{2}[(a + c)^2 - b^2] = \frac{1}{2}[(a^2 + 2ac + c^2) - b^2]$，
∴ 2ac = a² + 2ac + c² - b²，
∴ a² + c² = b²，
∴ △ABC 是直角三角形。

13. 如图17-26,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取$∠ABD= 120^{\circ },BD= 520m,∠D= 30^{\circ }$,那么另一边开挖点E离D多远,正好使A,C,E三点在一条直线上?($\sqrt {3}$取1.732,结果取整数)

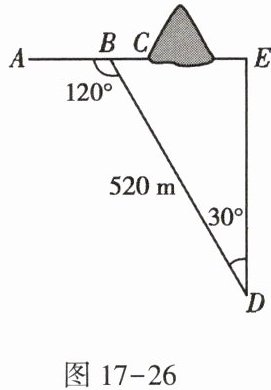
450m

答案：
∵ ∠ABD = 120°，∠D = 30°，
∴ ∠AED = 120° - 30° = 90°。在 Rt△BDE 中，BD = 520 m，∠D = 30°，
∴ $BE = \frac{1}{2}BD = 260$ m，
∴ $DE = \sqrt{BD^2 - BE^2} = 260\sqrt{3} ≈ 450$(m)。
∴ 另一边开挖点 E 离 D 约 450 m，正好使 A，C，E 三点在一条直线上。