1. 三角形的三条边长分别为$3cm$、$5cm$、$xcm$,则此三角形的周长$y$(单位:$cm$)与$x$(单位:$cm$)之间的函数关系式是
$y = x + 8 (2 < x < 8)$
.
答案:
1. $y = x + 8 (2 < x < 8)$
2. 若直线$l_1经过点(0,4)$,$l_2经过点(3,2)$,且$l_1与l_2关于x$轴对称,则$l_1与l_2$的交点坐标为
$(2, 0)$
.
答案:
2. $(2, 0)$
3. 在“看图说故事”活动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离$y$(单位:$km$)与他所用的时间$x$(单位:$\min$)的关系如图19-8所示:
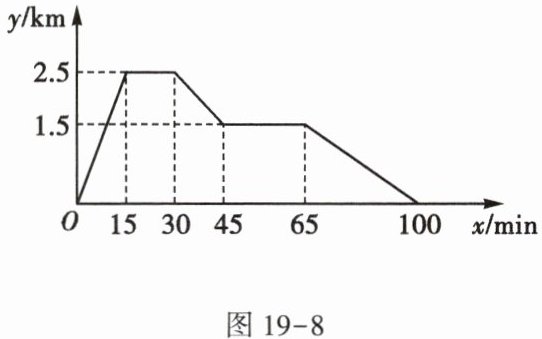
(1) 小明家离体育场的距离为
(2) 当$15≤x≤45$时,请直接写出$y关于x$的函数表达式;
(3) 当小明离家$2km$时,求他离开家所用的时间.

(1) 小明家离体育场的距离为
2.5
$km$,小明跑步的平均速度为$\frac{1}{6}$
$km/\min$;(2) 当$15≤x≤45$时,请直接写出$y关于x$的函数表达式;
当 $15 \leq x \leq 45$ 时,$y$ 关于 $x$ 的函数表达式为 $y = \begin{cases} 2.5 (15 \leq x \leq 30), \\ -\frac{1}{15}x + 4.5 (30 < x \leq 45). \end{cases}$
(3) 当小明离家$2km$时,求他离开家所用的时间.
当 $y = 2$ 时:① $\frac{1}{6}x = 2$,解得 $x = 12$;② $-\frac{1}{15}x + 4.5 = 2$,解得 $x = \frac{75}{2}$. 所以当小明离家 $2km$ 时,他离开家所用的时间为 $12min$ 或 $\frac{75}{2}min$.
答案:
3.
(1) 2.5 $\frac{1}{6}$
(2) 当 $15 \leq x \leq 45$ 时,$y$ 关于 $x$ 的函数表达式为 $y = \begin{cases} 2.5 (15 \leq x \leq 30), \\ -\frac{1}{15}x + 4.5 (30 < x \leq 45). \end{cases}$
(3) 当 $y = 2$ 时:① $\frac{1}{6}x = 2$,解得 $x = 12$;② $-\frac{1}{15}x + 4.5 = 2$,解得 $x = \frac{75}{2}$. 所以当小明离家 $2km$ 时,他离开家所用的时间为 $12min$ 或 $\frac{75}{2}min$.
(1) 2.5 $\frac{1}{6}$
(2) 当 $15 \leq x \leq 45$ 时,$y$ 关于 $x$ 的函数表达式为 $y = \begin{cases} 2.5 (15 \leq x \leq 30), \\ -\frac{1}{15}x + 4.5 (30 < x \leq 45). \end{cases}$
(3) 当 $y = 2$ 时:① $\frac{1}{6}x = 2$,解得 $x = 12$;② $-\frac{1}{15}x + 4.5 = 2$,解得 $x = \frac{75}{2}$. 所以当小明离家 $2km$ 时,他离开家所用的时间为 $12min$ 或 $\frac{75}{2}min$.
4. 为增强公民的节约意识,合理利用天然气资源,某市自$1月1$日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如下表所示:
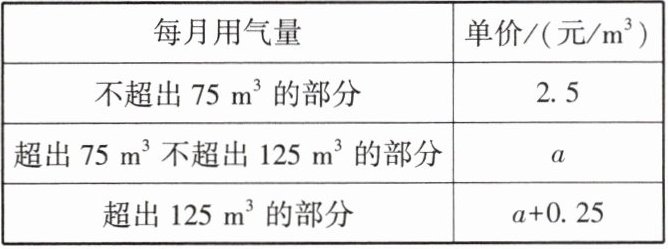
(1) 若甲用户$3月份的用气量为60m^3$,则应缴费
(2) 若调价后每月支出的燃气费为$y$(单位:元),每月的用气量为$x$(单位:$m^3$),$y与x$之间的关系如图19-9所示,求$a的值及y与x$之间的函数关系式;
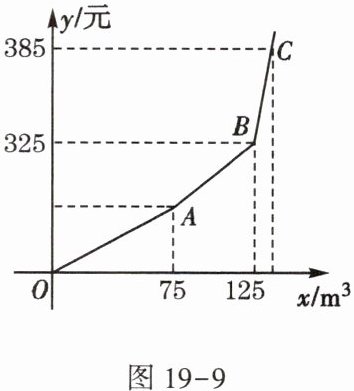
(3) 在(2)的条件下,若乙用户$2$,$3月份共用气175m^3$(3月份用气量

(1) 若甲用户$3月份的用气量为60m^3$,则应缴费
150
元;(2) 若调价后每月支出的燃气费为$y$(单位:元),每月的用气量为$x$(单位:$m^3$),$y与x$之间的关系如图19-9所示,求$a的值及y与x$之间的函数关系式;

$a = (325 - 75 × 2.5) ÷ (125 - 75) = 2.75$,$a + 0.25 = 3$,线段 $OA$ 的函数关系式为 $y = 2.5x (0 \leq x \leq 75)$. 线段 $AB$ 的函数关系式为 $y = (x - 75) × 2.75 + 2.5 × 75$,即 $y = 2.75x - 18.75 (75 < x \leq 125)$. 射线 $BC$ 的函数关系式为 $y = 325 + (x - 125) × 3$,即 $y = 3x - 50 (x > 125)$.
(3) 在(2)的条件下,若乙用户$2$,$3月份共用气175m^3$(3月份用气量
低
于
2月份用气量),共缴费$455$元,乙用户$2$,$3$月份的用气量各是多少?设乙用户 2 月份用气 $x m^3$,则 3 月份用气 $(175 - x) m^3$. ① 当 $x > 125$,$175 - x \leq 75$ 时,$3x - 50 + 2.5 (175 - x) = 455$,解得 $x = 135$,$175 - x = 40$,符合题意. ② 当 $75 < x \leq 125$,$175 - x \leq 75$ 时,$2.75x - 18.75 + 2.5 (175 - x) = 455$,解得 $x = 145$,不符合题意,舍去. ③ 当 $75 < x \leq 125$,$75 < 175 - x \leq 125$ 时,$2.75x - 18.75 + 2.75 (175 - x) - 18.75 = 455$,此方程无解. 所以乙用户 2,3 月份的用气量分别是 $135 m^3$,$40 m^3$.
答案:
4.
(1) 150
(2) $a = (325 - 75 × 2.5) ÷ (125 - 75) = 2.75$,$a + 0.25 = 3$,线段 $OA$ 的函数关系式为 $y = 2.5x (0 \leq x \leq 75)$. 线段 $AB$ 的函数关系式为 $y = (x - 75) × 2.75 + 2.5 × 75$,即 $y = 2.75x - 18.75 (75 < x \leq 125)$. 射线 $BC$ 的函数关系式为 $y = 325 + (x - 125) × 3$,即 $y = 3x - 50 (x > 125)$.
(3) 设乙用户 2 月份用气 $x m^3$,则 3 月份用气 $(175 - x) m^3$. ① 当 $x > 125$,$175 - x \leq 75$ 时,$3x - 50 + 2.5 (175 - x) = 455$,解得 $x = 135$,$175 - x = 40$,符合题意. ② 当 $75 < x \leq 125$,$175 - x \leq 75$ 时,$2.75x - 18.75 + 2.5 (175 - x) = 455$,解得 $x = 145$,不符合题意,舍去. ③ 当 $75 < x \leq 125$,$75 < 175 - x \leq 125$ 时,$2.75x - 18.75 + 2.75 (175 - x) - 18.75 = 455$,此方程无解. 所以乙用户 2,3 月份的用气量分别是 $135 m^3$,$40 m^3$.
(1) 150
(2) $a = (325 - 75 × 2.5) ÷ (125 - 75) = 2.75$,$a + 0.25 = 3$,线段 $OA$ 的函数关系式为 $y = 2.5x (0 \leq x \leq 75)$. 线段 $AB$ 的函数关系式为 $y = (x - 75) × 2.75 + 2.5 × 75$,即 $y = 2.75x - 18.75 (75 < x \leq 125)$. 射线 $BC$ 的函数关系式为 $y = 325 + (x - 125) × 3$,即 $y = 3x - 50 (x > 125)$.
(3) 设乙用户 2 月份用气 $x m^3$,则 3 月份用气 $(175 - x) m^3$. ① 当 $x > 125$,$175 - x \leq 75$ 时,$3x - 50 + 2.5 (175 - x) = 455$,解得 $x = 135$,$175 - x = 40$,符合题意. ② 当 $75 < x \leq 125$,$175 - x \leq 75$ 时,$2.75x - 18.75 + 2.5 (175 - x) = 455$,解得 $x = 145$,不符合题意,舍去. ③ 当 $75 < x \leq 125$,$75 < 175 - x \leq 125$ 时,$2.75x - 18.75 + 2.75 (175 - x) - 18.75 = 455$,此方程无解. 所以乙用户 2,3 月份的用气量分别是 $135 m^3$,$40 m^3$.
查看更多完整答案,请扫码查看


