《2025年暑假作业本大象出版社八年级数学人教版》

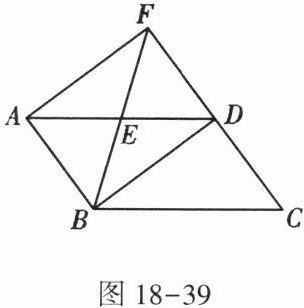
13. 如图18-39,在平行四边形$ABCD$中,连接$BD$,$E为线段AD$的中点,延长$BE与CD的延长线交于点F$,连接$AF$,$∠BDF= 90^{\circ }$.
(1)求证:四边形$ABDF$是矩形;
(2)若$AD= 5,DF= 3$,求四边形$ABCF的面积S$为18.

答案：
(1)
∵ 四边形 $ A B C D $ 是平行四边形，
∴ $ B A // C D $，
∴ $ \angle B A E = \angle F D E $。
∵ $ E $ 为线段 $ A D $ 的中点，
∴ $ A E = D E $。在 $ \triangle B E A $ 和 $ \triangle F E D $ 中，
$\left\{ \begin{array} { l } { \angle B A E = \angle F D E } \\ { A E = D E } \\ { \angle B E A = \angle F E D } \end{array} \right.$
∴ $ \triangle B E A \cong \triangle F E D ( A S A ) $，
∴ $ E F = E B $。又
∵ $ A E = D E $，
∴ 四边形 $ A B D F $ 是平行四边形。
∵ $ \angle B D F = 90 ^ { \circ } $，
∴ 四边形 $ A B D F $ 是矩形。
(2) 由
(1) 得，四边形 $ A B D F $ 是矩形，
∴ $ \angle A F D = 90 ^ { \circ } $，$ A B = D F = 3 $，$ A F = B D $，
∴ $ A F = \sqrt { A D ^ { 2 } - D F ^ { 2 } } = \sqrt { 5 ^ { 2 } - 3 ^ { 2 } } = 4 $，
∴ $ S _ { \text { 矩形 } A B D F } = D F \cdot A F = 3 × 4 = 12 $，$ B D = A F = 4 $。
∵ 四边形 $ A B C D $ 是平行四边形，
∴ $ C D = A B = 3 $，
∴ $ S _ { \triangle B C D } = \frac { 1 } { 2 } B D \cdot C D = \frac { 1 } { 2 } × 4 × 3 = 6 $，
∴ 四边形 $ A B C F $ 的面积 $ S = S _ { \text { 矩形 } A B D F } + S _ { \triangle B C D } = 12 + 6 = 18 $，即四边形 $ A B C F $ 的面积 $ S $ 为 18。

1. 如图18-40,在$\triangle ABC$中,$D$,$E$,$F分别是BC$,$AC$,$AB$的中点.若$AB = 6$,$BC = 8$,则四边形$BDEF$的周长是(B)
A.28
B.14
C.10
D.7

答案： B

2. 如图18-41,在矩形$ABCD$中,$AB = 6$,$BC = 8$,过对角线交点$O作EF\perp AC分别交AD于点E$,交$BC于点F$,则$DE$的长是(B)
A.1
B.$\frac{7}{4}$
C.2
D.$\frac{12}{5}$

答案： B

3. 如图18-42,在矩形$ABCD$中,$AD ＞ AB$,点$E$,$F分别在AD$,$BC$边上,$EF// AB$,$AE = AB$,$AF与BE相交于点O$,连接$OC$.若$BF = 2CF$,则$OC与EF$之间的数量关系正确的是(A)
A.$2OC = \sqrt{5}EF$
B.$\sqrt{5}OC = 2EF$
C.$2OC = \sqrt{3}EF$
D.$OC = EF$

答案： A