1. 已知$□ ABCD$中,$∠B = 4∠A$,则$∠C$等于(
A.$18^{\circ}$
B.$36^{\circ}$
C.$72^{\circ}$
D.$144^{\circ}$
B
)A.$18^{\circ}$
B.$36^{\circ}$
C.$72^{\circ}$
D.$144^{\circ}$
答案:
B
2. 如图18-1,$□ ABCD的对角线AC与BD相交于点O$,且$AC + BD = 16$,$CD = 6$,则$\triangle ABO$的周长是(
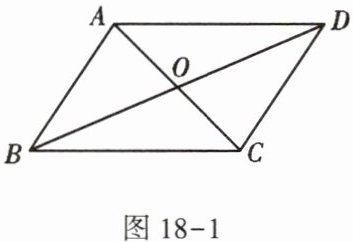
A.10
B.14
C.20
D.22
B
)
A.10
B.14
C.20
D.22
答案:
B
3. 已知一个平行四边形的一条对角线将其分为全等的两个等腰直角三角形,且这条对角线的长为6,则另一条对角线的长为
6或$6\sqrt{5}$
.
答案:
6或$6\sqrt{5}$
4. 如图18-2,在$□ ABCD$中,$DF平分∠ADC$,交$AB于点F$,$BE// DF$,交$AD的延长线于点E$. 若$∠A = 40^{\circ}$,求$∠ABE$的度数.
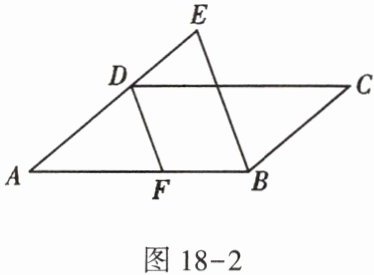
∵ 四边形ABCD是平行四边形,∴ AB//CD,∴ ∠A + ∠ADC = 180°。∵ ∠A = 40°,∴ ∠ADC =

∵ 四边形ABCD是平行四边形,∴ AB//CD,∴ ∠A + ∠ADC = 180°。∵ ∠A = 40°,∴ ∠ADC =
140°
。∵ DF平分∠ADC,∴ ∠CDF = $\frac{1}{2}$∠ADC = 70°
,∴ ∠AFD = ∠CDF = 70°
。∵ DF//BE,∴ ∠ABE = ∠AFD = 70°
。
答案:
∵ 四边形ABCD是平行四边形,
∴ AB//CD,
∴ ∠A + ∠ADC = 180°。
∵ ∠A = 40°,
∴ ∠ADC = 140°。
∵ DF平分∠ADC,
∴ ∠CDF = $\frac{1}{2}$∠ADC = 70°,
∴ ∠AFD = ∠CDF = 70°。
∵ DF//BE,
∴ ∠ABE = ∠AFD = 70°。
∵ 四边形ABCD是平行四边形,
∴ AB//CD,
∴ ∠A + ∠ADC = 180°。
∵ ∠A = 40°,
∴ ∠ADC = 140°。
∵ DF平分∠ADC,
∴ ∠CDF = $\frac{1}{2}$∠ADC = 70°,
∴ ∠AFD = ∠CDF = 70°。
∵ DF//BE,
∴ ∠ABE = ∠AFD = 70°。
5. 如图18-3,在$□ ABCD$中,$E$,$G$,$H$,$F分别是AB$,$BC$,$CD$,$DA$上的点,且$BE = DH$,$AF = CG$. 求证:$EF = HG$.
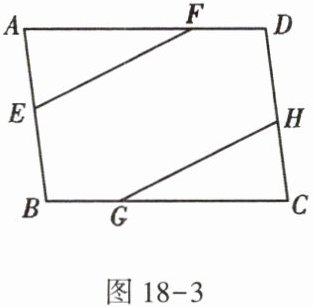
证明:

证明:
∵ 四边形ABCD是平行四边形,∴ AB = CD,∠A = ∠C。∵ BE = DH,∴ AB - BE = CD - DH,即AE = CH。在△AEF和△CHG中,$\left\{\begin{array}{l}AE = CH,\\\angle A = \angle C,\\AF = CG,\end{array}\right.$ ∴ △AEF ≌ △CHG(SAS),∴ EF = HG。
答案:
∵ 四边形ABCD是平行四边形,
∴ AB = CD,∠A = ∠C。
∵ BE = DH,
∴ AB - BE = CD - DH,即AE = CH。在△AEF和△CHG中,$\left\{\begin{array}{l}AE = CH,\\\angle A = \angle C,\\AF = CG,\end{array}\right.$
∴ △AEF ≌ △CHG(SAS),
∴ EF = HG。
∵ 四边形ABCD是平行四边形,
∴ AB = CD,∠A = ∠C。
∵ BE = DH,
∴ AB - BE = CD - DH,即AE = CH。在△AEF和△CHG中,$\left\{\begin{array}{l}AE = CH,\\\angle A = \angle C,\\AF = CG,\end{array}\right.$
∴ △AEF ≌ △CHG(SAS),
∴ EF = HG。
查看更多完整答案,请扫码查看


