《2025年暑假活动实践与思考八年级理综通用版》

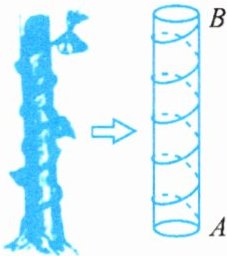
10. 我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意：如图所示，把枯木看作一个圆柱体，因一丈是10尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点$A$处缠绕而上，绕五周后其末端恰好到达点$B$处，则问题中葛藤的最短长度是25尺.

答案： 25

11. 已知在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\angle B = 30^{\circ}$，$AC = 1$，点$D$在斜边$AB$上，将$Rt\triangle ABC$沿着过点$D$的一条直线翻折，使点$B$落在射线$BC$上的$B'$处，连接$DB'$，$AB'$.
（1）当$D$是$AB$的中点时，$S_{\triangle AB'D}=$$\frac{\sqrt{3}}{4}$；
（2）当$\triangle AB'D$是直角三角形时，$AD$的长是$\frac{4}{3}$或$\frac{2}{3}$.

答案：
(1)$\frac{\sqrt{3}}{4}$　
(2)$\frac{4}{3}$或$\frac{2}{3}$

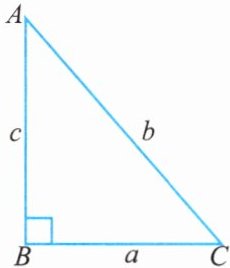
12. 如图所示，在$Rt\triangle ABC$中，$AB = c$，$BC = a$，$AC = b$，$\angle B = 90^{\circ}$.
（1）已知$b = 8$，$c = 4$，求$a$；$4\sqrt{3}$
（2）已知$b = \sqrt{5}$，$a:c = 1:2$，求$a$，$c$.$a=1$，$c=2$

答案：

$解：(1)∵∠B=90°，$

$∴a=\sqrt {b^2-c^2}=\sqrt {8^2-4^2}=\sqrt {48}=4\sqrt 3 .$

$(2)在Rt△ABC中，根据勾股定理， a²+c²=b².$

$∵b=\sqrt{5}，a:c=1:2，$

$∴a²+4a²=5，$

$∴a=1，c=2.$

13. 勾股定理是初等几何中最重要的定理之一，它的证明方法很多，如图1所示是3世纪我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，通过对图形的切割、拼接，巧妙地利用面积关系证明了勾股定理.
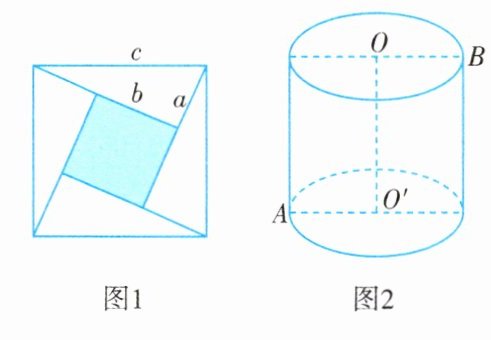
（1）定理证明：图1是由四个全等的直角三角形围成的一个大正方形，中间的部分是一个小正方形（阴影）.如果直角三角形较小的直角边长为$a$，较大的直角边长为$b$，斜边长为$c$，请你根据图1证明勾股定理；
（2）问题解决：如图2所示，圆柱的底面半径为40cm，高为$30\pi cm$，蚂蚁在圆柱表面爬行，从点$A$爬到点$B$的最短路程是多少厘米？（结果保留$\pi$）

答案：
解:
(1)
∵阴影部分的面积=大正方形面积−4×直角三角形面积，
∴(b−a)²=c²−4×$\frac{1}{2}$ab.
∴a²−2ab+b²=c²−2ab.
∴a²+b²=c²;
(2)圆柱侧面展开图如图所示.
　　　　　　
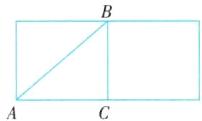
　根据圆柱的底面半径为40cm,得出AC=$\frac{2×40π}{2}$=40π.
∵高为30π，
∴AB=$\sqrt{AC²+BC²}$=50π(cm).
∴从点A爬到点B的最短路程是50π厘米.