1. 平行四边形具有而一般四边形不一定具有的性质是 (
A. 内角和等于 $ 360^{\circ} $
B. 外角和等于 $ 360^{\circ} $
C. 不稳定
D. 对角线互相平分
D
)A. 内角和等于 $ 360^{\circ} $
B. 外角和等于 $ 360^{\circ} $
C. 不稳定
D. 对角线互相平分
答案:
D
2. 在 $ □ ABCD $ 中,对角线 $ AC $,$ BD $ 相交于点 $ O $,则下列结论:① $ OA = OC $;② $ \angle BAD = \angle BCD $;③ $ AD = BC $;④ $ \angle BAD + \angle ABC = 180^{\circ} $。其中正确的有 (
A. 4 个
B. 3 个
C. 2 个
D. 1 个
A
)A. 4 个
B. 3 个
C. 2 个
D. 1 个
答案:
A
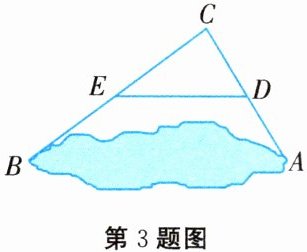
3. 如图所示,数学活动课上,某兴趣小组要测量池塘两端 $ A $,$ B $ 的距离,他们先在平地上取一个点 $ C $,从点 $ C $ 不经过池塘可以直接到达点 $ A $ 和点 $ B $,连接 $ AC $,$ BC $,分别找出 $ AC $,$ BC $ 的中点 $ D $,$ E $,连接 $ DE $,并量出 $ DE = 24 \mathrm{~m} $,则 $ A $,$ B $ 的距离为 (
A. $ 48 \mathrm{~m} $
B. $ 60 \mathrm{~m} $
C. $ 80 \mathrm{~m} $
D. 不能确定
A
)
A. $ 48 \mathrm{~m} $
B. $ 60 \mathrm{~m} $
C. $ 80 \mathrm{~m} $
D. 不能确定
答案:
A
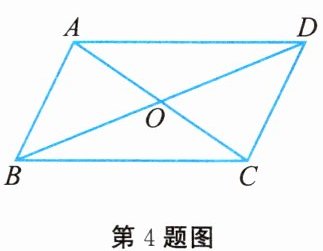
4. 如图所示,在四边形 $ ABCD $ 中,对角线 $ AC $,$ BD $ 相交于点 $ O $,下列条件不能判定这个四边形是平行四边形的是 (
A. $ AB // DC $,$ AD // BC $
B. $ OA = OC $,$ OB = OD $
C. $ AD = BC $,$ AB // DC $
D. $ AB = DC $,$ AD = BC $
C
)
A. $ AB // DC $,$ AD // BC $
B. $ OA = OC $,$ OB = OD $
C. $ AD = BC $,$ AB // DC $
D. $ AB = DC $,$ AD = BC $
答案:
C
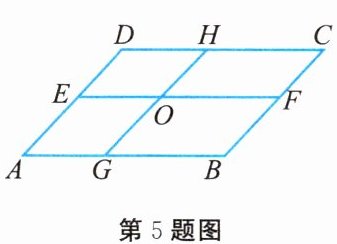
5. 如图所示,在 $ □ ABCD $ 中,$ EF // AB $,$ GH // AD $,$ EF $ 与 $ GH $ 交于点 $ O $,则图中的平行四边形共有 (
A. 7 个
B. 8 个
C. 9 个
D. 11 个
C
)
A. 7 个
B. 8 个
C. 9 个
D. 11 个
答案:
C
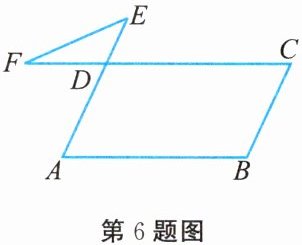
6. 如图所示,在 $ □ ABCD $ 中,$ \angle B = 110^{\circ} $,延长 $ CD $ 至点 $ F $,延长 $ AD $ 至点 $ E $,连接 $ EF $,则 $ \angle E + \angle F $ 的值为 (
A. $ 110^{\circ} $
B. $ 70^{\circ} $
C. $ 50^{\circ} $
D. $ 30^{\circ} $
B
)
A. $ 110^{\circ} $
B. $ 70^{\circ} $
C. $ 50^{\circ} $
D. $ 30^{\circ} $
答案:
B
7. 已知,在四边形 $ ABCD $ 中,$ \angle A = \angle C = 55^{\circ} $,当 $ \angle B = $
125°
时,四边形是平行四边形。
答案:
125°
8. 如图所示,在平面直角坐标系中,平行四边形 $ OABC $ 的顶点 $ O(0,0) $,$ A(5,0) $,$ B(2,3) $,则顶点 $ C $ 的坐标是
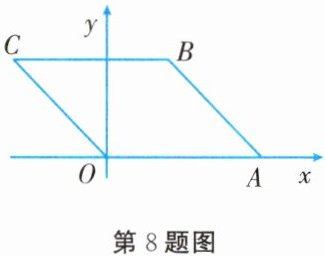
(−3,3)
。
答案:
(−3,3)
查看更多完整答案,请扫码查看


