《2025年暑假活动实践与思考八年级理综通用版》

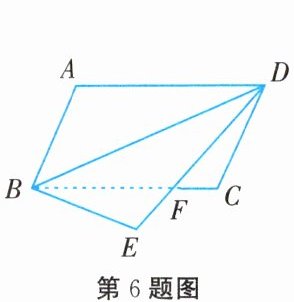
6. 如图所示，将平行四边形 $ABCD$ 沿对角线 $BD$ 折叠，使点 $A$ 落在点 $E$ 处，$ED$ 交 $BC$ 于点 $F$。若 $\angle ABD = 48^{\circ}$，$\angle CFD = 40^{\circ}$，则 $\angle E$ 的度数为______$112^{\circ}$。

答案： 6. $ 112 ^ { \circ } $

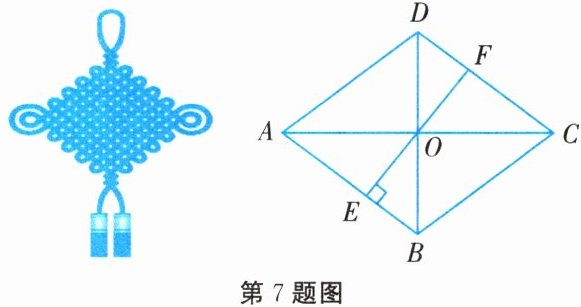
7. 中国结寓意团圆、美满，以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴。如图所示，小陶家有一个菱形中国结装饰，测得 $BD = 12\mathrm{cm}$，$AC = 16\mathrm{cm}$，直线 $EF\perp AB$ 交两对边于点 $E$，$F$，则 $EF$ 的长为$\frac { 48 } { 5 } \mathrm { cm }$。

答案： 7. $ \frac { 48 } { 5 } \mathrm { cm } $

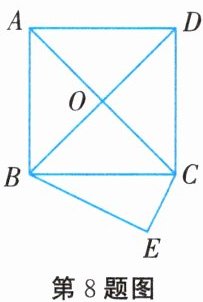
8. 如图所示，正方形 $ABCD$ 的对角线交于点 $O$，$E$ 是正方形外一点，且 $BE\perp CE$。若 $BE = 6$，$BC = 3CE$，则 $BD$ 的长为______9。

答案： 8. 9

9. 如图所示，菱形 $ABCD$ 的对角线 $AC$，$BD$ 相交于点 $O$，过点 $D$ 作 $DE// AC$ 且 $DE=\frac{1}{2}AC$，连接 $AE$ 交 $OD$ 于点 $F$，连接 $CE$，$OE$。
（1）求证：四边形 $OCED$ 为矩形；
（2）若菱形 $ABCD$ 的边长为 12，$\angle ABC = 60^{\circ}$，求 $\triangle ADE$ 的面积。
（1）证明：
- 因为四边形$ABCD$是菱形，根据菱形的性质可知$AC\perp BD$，$OA = OC=\frac{1}{2}AC$。
- 已知$DE// AC$且$DE=\frac{1}{2}AC$，所以$DE = OC$。
- 又因为$DE// AC$，根据“一组对边平行且相等的四边形是平行四边形”，可得四边形$OCED$是平行四边形。
- 由于$AC\perp BD$，即$\angle DOC = 90^{\circ}$。
- 根据“有一个角是直角的平行四边形是矩形”，所以四边形$OCED$为矩形。
（2）解：
- 因为四边形$ABCD$是菱形，$\angle ABC = 60^{\circ}$，$AB = BC = 12$，所以$\triangle ABC$是等边三角形。
- 根据等边三角形的性质，$AC = AB = 12$。
- 因为菱形的对角线互相垂直平分，所以$AO=\frac{1}{2}AC = 6$，$BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{12^{2}-6^{2}}=\sqrt{144 - 36}=\sqrt{108}=6\sqrt{3}$，$BD = 2BO = 12\sqrt{3}$。
- 因为四边形$OCED$是矩形，所以$CE = OD=\frac{1}{2}BD = 6\sqrt{3}$，$DE = OC = 6$。
- 又因为$DE// AC$，所以$S_{\triangle ADE}=S_{\triangle CDE}$（等底等高的三角形面积相等，以$DE$为底，$DE$到$AC$的距离相等）。
- 根据矩形面积公式$S = 长×宽$，$S_{OCED}=OC× OD=6×6\sqrt{3}=36\sqrt{3}$。
- 因为$S_{\triangle CDE}=\frac{1}{2}S_{OCED}$（矩形的对角线将矩形分成两个面积相等的三角形），所以$S_{\triangle ADE}=\frac{1}{2}×36\sqrt{3}=18\sqrt{3}$。
故$\triangle ADE$的面积为$18\sqrt{3}$。

答案： $(1)$ 证明四边形$OCED$为矩形
解：
- 因为四边形$ABCD$是菱形，根据菱形的性质可知$AC\perp BD$，$OA = OC=\frac{1}{2}AC$。
- 已知$DE// AC$且$DE=\frac{1}{2}AC$，所以$DE = OC$。
- 又因为$DE// AC$，根据“一组对边平行且相等的四边形是平行四边形”，可得四边形$OCED$是平行四边形。
- 由于$AC\perp BD$，即$\angle DOC = 90^{\circ}$。
- 根据“有一个角是直角的平行四边形是矩形”，所以四边形$OCED$为矩形。
$(2)$ 求$\triangle ADE$的面积
解：
- 因为四边形$ABCD$是菱形，$\angle ABC = 60^{\circ}$，$AB = BC = 12$，所以$\triangle ABC$是等边三角形。
- 根据等边三角形的性质，$AC = AB = 12$。
- 因为菱形的对角线互相垂直平分，所以$AO=\frac{1}{2}AC = 6$，$BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{12^{2}-6^{2}}=\sqrt{144 - 36}=\sqrt{108}=6\sqrt{3}$，$BD = 2BO = 12\sqrt{3}$。
- 因为四边形$OCED$是矩形，所以$CE = OD=\frac{1}{2}BD = 6\sqrt{3}$，$DE = OC = 6$。
- 又因为$DE// AC$，所以$S_{\triangle ADE}=S_{\triangle CDE}$（等底等高的三角形面积相等，以$DE$为底，$DE$到$AC$的距离相等）。
- 根据矩形面积公式$S = 长\times宽$，$S_{OCED}=OC\times OD=6\times6\sqrt{3}=36\sqrt{3}$。
- 因为$S_{\triangle CDE}=\frac{1}{2}S_{OCED}$（矩形的对角线将矩形分成两个面积相等的三角形），所以$S_{\triangle ADE}=\frac{1}{2}\times36\sqrt{3}=18\sqrt{3}$。
综上，$(1)$ 四边形$OCED$为矩形得证；$(2)$ $\triangle ADE$的面积为$18\boldsymbol{\sqrt{3}}$。

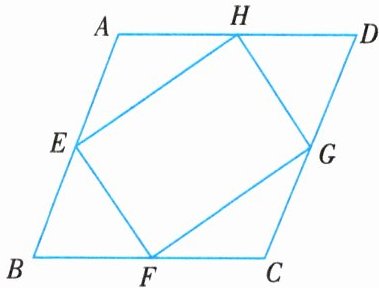
10. 如图所示，在四边形 $ABCD$ 中，点 $E$，$F$，$G$，$H$ 分别是各边的中点，且 $AB// CD$，$AD// BC$，四边形 $EFGH$ 是矩形。
（1）求证：四边形 $ABCD$ 是菱形；
（2）若矩形 $EFGH$ 的周长为 22，四边形 $ABCD$ 的面积为 10，求 $AB$ 的长。

答案：
10.
(1)证明:略;
(提示:连接 $ A C $, $ B D $ 相交于点 $ O $.)

(2)解: $ \because $ 在四边形 $ A B C D $ 中, 点 $ E $, $ F $, $ G $, $ H $ 分别是各边的中点,
$ \therefore G F = E H = \frac { 1 } { 2 } B D $, $ G H = E F = \frac { 1 } { 2 } A C $.
$ \because $ 矩形 $ E F G H $ 的周长为 22,
$ \therefore B D + A C = 22 $.
$ \because $ 四边形 $ A B C D $ 是菱形,
$ \therefore \frac { 1 } { 2 } B D + \frac { 1 } { 2 } A C = O A + O B = 11 $.
$ \because $ 四边形 $ A B C D $ 的面积为 10,
$ \therefore \frac { 1 } { 2 } B D \cdot A C = 10 $, 即 $ 2 O A \cdot O B = 10 $.
$ \because ( O A + O B ) ^ { 2 } = O A ^ { 2 } + 2 O A \cdot O B + O B ^ { 2 } = 121 $,
$ \therefore O A ^ { 2 } + O B ^ { 2 } = 121 - 10 = 111 $.
$ \therefore A B = \sqrt { O A ^ { 2 } + O B ^ { 2 } } = \sqrt { 111 } $.