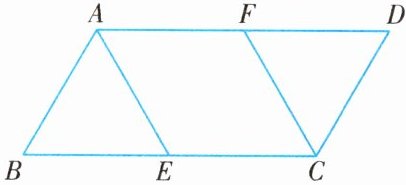
14. 如图所示,平行四边形 ABCD 中,AE,CF 分别是$\angle BAD$,$\angle BCD$的平分线,且 E,F 分别在边 BC,AD 上,$AE = AF$.
(1)求证:四边形 AECF 是菱形;
(2)若$\angle ABC = 60^{\circ}$,$\triangle ABE$的面积等于$4\sqrt{3}$,求平行线 AB 与 DC 间的距离.
(1)求证:四边形 AECF 是菱形;
(2)若$\angle ABC = 60^{\circ}$,$\triangle ABE$的面积等于$4\sqrt{3}$,求平行线 AB 与 DC 间的距离.
$4\sqrt{3}$

答案:
(1) 证明:
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB,BC//AD.
∴∠FAE=∠BEA.
∵AE,CF分别是∠BAD,∠BCD的 平分线,
∴∠FAE=$\frac{1}{2}$∠BAD,∠FCE=$\frac{1}{2}$∠BCD.
∴∠FAE=∠FCE.
∴∠BEA=∠FCE.
∴AE//FC.
∴EC//AF.
∴四边形AECF是平行四边形,
∴四边形AECF是菱形.
(2) 解:连接 EF. 根据题意,得
$ \angle A B C = \angle C D A = 60 ^ { \circ } $,$ \angle B A D = 120 ^ { \circ } $。
∵ AE 是 $ \angle B A D $ 的平分线,$ A E = A F $,
$ \therefore \angle B A E = \angle E A F = 60 ^ { \circ } $。
$ \therefore \triangle A B E $,$ \triangle A E F $ 是等边三角形。
$ \therefore A B = A E $。
$ \therefore \triangle A B E $,$ \triangle A E F $ 是边长等于 AB 的等边三角形。
同理可证 $ \triangle C D F $,$ \triangle C E F $ 是边长等于 CD 的等边三角形。
∵ 四边形 ABCD 是平行四边形,
$ \therefore A B = C D $。
$ \therefore \triangle A B E $,$ \triangle A E F $,$ \triangle C E F $,$ \triangle C D F $ 是边长等于 AB 的等边三角形。
由 $ \triangle A B E $ 的面积等于 $ 4 \sqrt { 3 } $ 得 $ A B = 4 $,且平行四边形 ABCD 的面积等于 $ 16 \sqrt { 3 } $。
设平行线 AB 与 DC 间的距离为 h,则
$ A B \times h = 4 h = 16 \sqrt { 3 } $,解得 $ h = 4 \sqrt { 3 } $。
$ \therefore $ 平行线 AB 与 CD 间的距离为 $ 4 \sqrt { 3 } $。
(1) 证明:
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB,BC//AD.
∴∠FAE=∠BEA.
∵AE,CF分别是∠BAD,∠BCD的 平分线,
∴∠FAE=$\frac{1}{2}$∠BAD,∠FCE=$\frac{1}{2}$∠BCD.
∴∠FAE=∠FCE.
∴∠BEA=∠FCE.
∴AE//FC.
又
∵E,F分别在边BC,AD上,
∵E,F分别在边BC,AD上,
∴EC//AF.
∴四边形AECF是平行四边形,
又
∵AE=AF,
∵AE=AF,
∴四边形AECF是菱形.
(2) 解:连接 EF. 根据题意,得
$ \angle A B C = \angle C D A = 60 ^ { \circ } $,$ \angle B A D = 120 ^ { \circ } $。
∵ AE 是 $ \angle B A D $ 的平分线,$ A E = A F $,
$ \therefore \angle B A E = \angle E A F = 60 ^ { \circ } $。
$ \therefore \triangle A B E $,$ \triangle A E F $ 是等边三角形。
$ \therefore A B = A E $。
$ \therefore \triangle A B E $,$ \triangle A E F $ 是边长等于 AB 的等边三角形。
同理可证 $ \triangle C D F $,$ \triangle C E F $ 是边长等于 CD 的等边三角形。
∵ 四边形 ABCD 是平行四边形,
$ \therefore A B = C D $。
$ \therefore \triangle A B E $,$ \triangle A E F $,$ \triangle C E F $,$ \triangle C D F $ 是边长等于 AB 的等边三角形。
由 $ \triangle A B E $ 的面积等于 $ 4 \sqrt { 3 } $ 得 $ A B = 4 $,且平行四边形 ABCD 的面积等于 $ 16 \sqrt { 3 } $。
设平行线 AB 与 DC 间的距离为 h,则
$ A B \times h = 4 h = 16 \sqrt { 3 } $,解得 $ h = 4 \sqrt { 3 } $。
$ \therefore $ 平行线 AB 与 CD 间的距离为 $ 4 \sqrt { 3 } $。
15. 云南鲜花饼远近闻名,为了更好地服务好顾客,昆明某鲜花店新购进了两种新款鲜花饼,相关信息如下表:
|种别|玫瑰鲜花饼|茉莉鲜花饼|
|--|--|--|
|进价/(元/盒)|30|45|
|备注|①不超过 1950 元购进两种鲜花饼共 50 盒;②茉莉鲜花饼不少于 20 盒.|
(1)已知茉莉鲜花饼的标价是玫瑰鲜花饼标价的 1.5 倍,若顾客用 750 元购买两种鲜花饼,能单独购买茉莉鲜花饼的数量恰好比单独购买玫瑰鲜花饼的数量少 5 盒,请求出玫瑰鲜花饼、茉莉鲜花饼两种鲜花饼的标价;
(2)为了让利给消费者,商店老板便调整了销售方案,茉莉鲜花饼按照标价 8 折销售,玫瑰鲜花饼价格不变,那么商店应如何进货才能获得最大利润?
|种别|玫瑰鲜花饼|茉莉鲜花饼|
|--|--|--|
|进价/(元/盒)|30|45|
|备注|①不超过 1950 元购进两种鲜花饼共 50 盒;②茉莉鲜花饼不少于 20 盒.|
(1)已知茉莉鲜花饼的标价是玫瑰鲜花饼标价的 1.5 倍,若顾客用 750 元购买两种鲜花饼,能单独购买茉莉鲜花饼的数量恰好比单独购买玫瑰鲜花饼的数量少 5 盒,请求出玫瑰鲜花饼、茉莉鲜花饼两种鲜花饼的标价;
(2)为了让利给消费者,商店老板便调整了销售方案,茉莉鲜花饼按照标价 8 折销售,玫瑰鲜花饼价格不变,那么商店应如何进货才能获得最大利润?
答案:
$解:(1)设玫瑰鲜花饼的标价为x 元/盒,则茉莉鲜花饼的标价为 1.5x 元/盒.$
(2) 设购进玫瑰鲜花饼 a 盒,则购进茉莉鲜花饼 $ ( 50 - a ) $ 盒. 商店利润为 W 元. 由题意,得
$ W = ( 50 - 30 ) a + ( 75 \times 0.8 - 45 ) ( 50 - a ) = 5 a + 750 $。
根据题意,得 $ \left\{ \begin{array} { l } { 30 a + 45 ( 50 - a ) \leq 1950 }, \\ { 50 - a \geq 20 }. \end{array} \right. $
解得 $ 20 \leq a \leq 30 $。
$ \because k = 5 > 0 $,$ \therefore W $ 随 a 的增大而增大。
$ \therefore $ 当 $ a = 30 $ 时,$ W _ { \text { 最大 } } = 5 \times 30 + 750 = 900 $(元)。
此时,$ 50 - a = 20 $(盒)。
答:购进玫瑰鲜花饼 30 盒,购进茉莉鲜花饼 20 盒,商店利润最大,最大利润为 900 元。
$由题意,得\frac {750}x-\frac{750}{1.5x}=5,解得x=50,$
$经检验x=50是原分式方程的解$
$∴1.5x=1.5×50=75(元).$
答:玫瑰鲜花饼的标价为 50 元/盒,茉莉鲜花饼的标价为 75 元/盒;(2) 设购进玫瑰鲜花饼 a 盒,则购进茉莉鲜花饼 $ ( 50 - a ) $ 盒. 商店利润为 W 元. 由题意,得
$ W = ( 50 - 30 ) a + ( 75 \times 0.8 - 45 ) ( 50 - a ) = 5 a + 750 $。
根据题意,得 $ \left\{ \begin{array} { l } { 30 a + 45 ( 50 - a ) \leq 1950 }, \\ { 50 - a \geq 20 }. \end{array} \right. $
解得 $ 20 \leq a \leq 30 $。
$ \because k = 5 > 0 $,$ \therefore W $ 随 a 的增大而增大。
$ \therefore $ 当 $ a = 30 $ 时,$ W _ { \text { 最大 } } = 5 \times 30 + 750 = 900 $(元)。
此时,$ 50 - a = 20 $(盒)。
答:购进玫瑰鲜花饼 30 盒,购进茉莉鲜花饼 20 盒,商店利润最大,最大利润为 900 元。
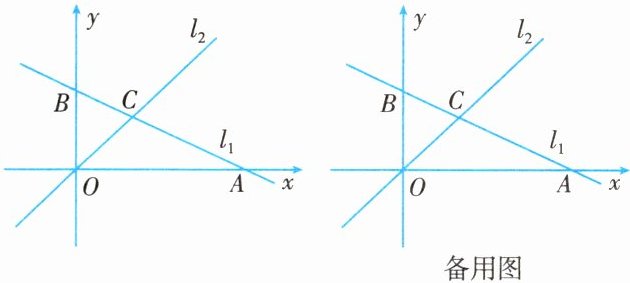
16. 如图所示,在平面直角坐标系中,直线$l_{1}$的解析式为$y = kx + b(k\neq0)$,直线$l_{2}$的解析式为$y = x$,直线$l_{1}$经过点$A(6,0)$,$B(0,3)$,直线$l_{1}$与$l_{2}$交于点 C.
(1)求直线$l_{1}$的解析式和$\triangle COB$的面积;
(2)在 x 轴上是否存在点 P,使得$\triangle POC$为等腰三角形?若存在,请求出点 P 的坐标;若不存在,请说明理由.
(1)求直线$l_{1}$的解析式和$\triangle COB$的面积;
(2)在 x 轴上是否存在点 P,使得$\triangle POC$为等腰三角形?若存在,请求出点 P 的坐标;若不存在,请说明理由.

答案:
解:
(1)(过程略)直线 $ l _ { 1 } $ 的解析式为 $ y = - \frac { 1 } { 2 } x + 3 $,$ \triangle C O B $ 的面积为 3;
(2) 在 x 轴上存在点 P,使得 $ \triangle P O C $ 为等腰三角形。
根据题意,共有三种情况,如备用图所示。

① 当点 O 为顶角顶点时,$ O P = O C $。
以点 O 为圆心,OC 长为半径的圆与 x 轴的两个交点 $ P _ { 1 } $,$ P _ { 2 } $ 就是此时的点 P。
易得,$ O C = 2 \sqrt { 2 } $。
$ \therefore $ 点 $ P _ { 1 } $ 的坐标为 $ ( - 2 \sqrt { 2 } , 0 ) $,点 $ P _ { 2 } $ 的坐标为 $ ( 2 \sqrt { 2 } , 0 ) $;
② 当点 C 为顶角顶点时,$ C P = C O $。
以点 C 为圆心,CO 长为半径的圆与 x 轴的交点 $ P _ { 3 } $ 就是此时的点 P。
易得,点 $ P _ { 3 } $ 的坐标为 $ ( 4 , 0 ) $;
③ 当点 P 为顶角顶点时,显然,OC 的垂直平分线与 x 轴的交点 $ P _ { 4 } $ 就是此时的点 P。
易得,点 $ P _ { 4 } $ 的坐标为 $ ( 2 , 0 ) $。
综上所述,满足条件的点 P 的坐标为 $ ( - 2 \sqrt { 2 } , 0 ) $ 或 $ ( 2 \sqrt { 2 } , 0 ) $ 或 $ ( 4 , 0 ) $ 或 $ ( 2 , 0 ) $。
解:
(1)(过程略)直线 $ l _ { 1 } $ 的解析式为 $ y = - \frac { 1 } { 2 } x + 3 $,$ \triangle C O B $ 的面积为 3;
(2) 在 x 轴上存在点 P,使得 $ \triangle P O C $ 为等腰三角形。
根据题意,共有三种情况,如备用图所示。

① 当点 O 为顶角顶点时,$ O P = O C $。
以点 O 为圆心,OC 长为半径的圆与 x 轴的两个交点 $ P _ { 1 } $,$ P _ { 2 } $ 就是此时的点 P。
易得,$ O C = 2 \sqrt { 2 } $。
$ \therefore $ 点 $ P _ { 1 } $ 的坐标为 $ ( - 2 \sqrt { 2 } , 0 ) $,点 $ P _ { 2 } $ 的坐标为 $ ( 2 \sqrt { 2 } , 0 ) $;
② 当点 C 为顶角顶点时,$ C P = C O $。
以点 C 为圆心,CO 长为半径的圆与 x 轴的交点 $ P _ { 3 } $ 就是此时的点 P。
易得,点 $ P _ { 3 } $ 的坐标为 $ ( 4 , 0 ) $;
③ 当点 P 为顶角顶点时,显然,OC 的垂直平分线与 x 轴的交点 $ P _ { 4 } $ 就是此时的点 P。
易得,点 $ P _ { 4 } $ 的坐标为 $ ( 2 , 0 ) $。
综上所述,满足条件的点 P 的坐标为 $ ( - 2 \sqrt { 2 } , 0 ) $ 或 $ ( 2 \sqrt { 2 } , 0 ) $ 或 $ ( 4 , 0 ) $ 或 $ ( 2 , 0 ) $。
查看更多完整答案,请扫码查看


